Question

9、正方体ABCD-A₁B₁C₁D₁，E，F分别是AA₁，CC₁的中点，P是CC₁上的动点（包括端点），过点E、D、P作正方体的截面，若截面为四边形，则P的轨迹是（　　）

A、线段C₁F

B、线段CF

C、线段CF和一点C₁

D、线段C₁F和一点C

Answer 1

分析：根据E，F分别是AA₁，CC₁的中点，结合正方体的结构特征，我们易结合线面平行的性质定理，求出平面PDE于BB₁的交点，分别P点在不同位置时，M点是否在线段BB₁上，即可得到答案．

解答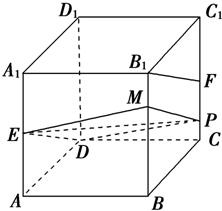：解：如图所示，
DE∥平面BB₁C₁C，
∴平面DEP与平面BB₁C₁C的交线PM∥ED，连接EM，
易证MP=ED，
∴MP∥ED，则M到达B₁时仍可构成四边形，即P到F．
而P在C₁F之间，不满足要求．
P到点C₁仍可构成四边形．
故选C．

点评：本题考查的知识点是棱柱的结构的特征，其中利用分类讨论思想，分别讨论P点在不同位置时，M点的位置是解答本题的关键．