题目内容
已知函数 .
.
(Ⅰ)当 时,求
时,求 的极小值;
的极小值;
(Ⅱ)若直线 对任意的
对任意的 都不是曲线
都不是曲线 的切线,求
的切线,求 的取值范围.
的取值范围.
【答案】
(Ⅰ)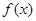 的极小值为
的极小值为 . (Ⅱ)
. (Ⅱ)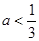 .
.
【解析】本试题主要是考查了导数在研究函数中的 运用。利用导数研究函数的单调性和极值问题,以及导数的几何意义求解切线方程的综合运用。
(1)利用当a=1,确定解析式然后求解导数,分析单调区间,得到其极值。
(2)因为要使直线对于任意的ms实数,x+y+m=0都不是曲线的切线,说米呢了导数值大于其斜率值
解:(Ⅰ)因为当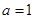 时,
时,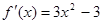 ,令
,令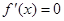 ,得
,得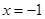 或
或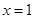 .
.
当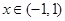 时,
时,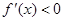 ;当
;当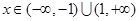 时,
时,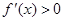 .所以
.所以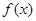 在
在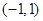 上单调递减,在
上单调递减,在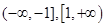 上单调递增. 所以
上单调递增. 所以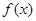 的极小值为
的极小值为 .
.
(Ⅱ)因为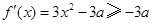 ,
,
所以,要使直线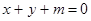 对任意的
对任意的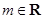 总
总
不是曲线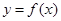 的切线,当且仅当
的切线,当且仅当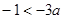 ,即
,即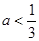 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|