题目内容
(本小题满分14分)
已知斜三棱柱ABC—A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α (0°<α<90°),点![]() 在底面上的射影
在底面上的射影![]() 落在
落在![]() 上.
上.
(1)求证:AC⊥平面BB1C1C;
(2)若AB1⊥BC1,D为BC的中点,求α ;
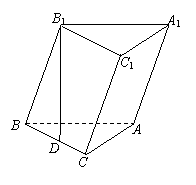 (3)若α = arccos ,且AC=BC=AA1时,求二面角C1—AB—C的大小.
(3)若α = arccos ,且AC=BC=AA1时,求二面角C1—AB—C的大小.
解 (1)∵ B1D⊥平面ABC, AC![]() 平面ABC,
平面ABC,
∴ B1D⊥AC, 又AC⊥BC, ![]() BC∩B1D=D.
BC∩B1D=D.
∴ AC⊥平面BB1C1C.
(2) ∵ AC⊥平面BB1C1C ,AB1⊥BC1 ,由三垂线定理可知,
B1C⊥BC1.
∴ 平行四边形BB1C1C为菱形,此时,BC=BB1.
又∵ B1D⊥BC,D为BC中点,B1C= B1B,∴△BB1C为正三角形,
∴ ∠B1BC= 60°.
(3)过C1作C1E⊥BC于E,则C1E⊥平面ABC.
过E作EF⊥AB于F,C1F,由三垂线定理,得C1F⊥AB.
∴∠C1FE是所求二面角C1—AB—C的平面角.
设AC=BC=AA1=a,
在Rt△CC1E中,由∠C1BE=α=![]() ,C1E=
,C1E=![]() a.
a.
在Rt△BEF中,∠EBF=45°,EF=![]() BE=
BE=![]() a.
a.
∴∠C1FE=45°,故所求的二面角C1—AB—C为45°.
解法二:(1)同解法一
(2)要使AB1⊥BC1,D是BC的中点,即![]() =0,||=||,
=0,||=||,
∴![]() ,
, ![]() =0,∴
=0,∴![]() .
.
∴![]() ,故△BB1C为正三角形,∠B1BC=60°;
,故△BB1C为正三角形,∠B1BC=60°;
∵ B1D⊥平面ABC,且D落在BC上,
∴ ∠B1BC即为侧棱与底面所成的角.
故当α=60°时,AB1⊥BC1,且D为BC中点.
(3)以C为原点,CA为x轴,CB为y轴,经过C点且垂直于平面ABC的直线为z轴建立空间直角坐标系,则A(a,0,0),B(0,a,0),C(0,-![]() ,
,![]() a),
a),
平面ABC的法向量n1=(0,0,1),设平面ABC1的法向量n2=(x,y,z).
由![]() n2=0,及
n2=0,及![]() n2=0,得
n2=0,得
∴n2=(![]() ,
,![]() ,1).
,1).
cos<n1, n2>= = ,
故n1 , n2所成的角为45°,即所求的二面角为45

 优学名师名题系列答案
优学名师名题系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)