题目内容
已知数列{an}的通项公式an=log2 (n∈N*),设其前n项和为Sn,则使Sn<-4成立的最小自然数n的值为 .
(n∈N*),设其前n项和为Sn,则使Sn<-4成立的最小自然数n的值为 .
【答案】分析:由已知中数列{an}的通项公式an=log2 (n∈N*),根据对数的运算性质,我们可以求出前n项和为Sn的表达式,解对数不等式可得n的值
(n∈N*),根据对数的运算性质,我们可以求出前n项和为Sn的表达式,解对数不等式可得n的值
解答:解:∵an=log2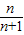
∴Sn=log2 +log2
+log2 +log2
+log2 +…log2
+…log2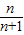 =log2(
=log2( •
• •
• •…•
•…•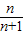 )=log2
)=log2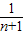
若Sn<-4,则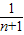
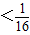
即n>15
则使Sn<-4成立的最小自然数n的值为16
故答案为:16
点评:本题考查的知识点是数列求和,对数的运算性质,对数不等式的解法,其中根据对数的运算性质求出Sn的表达式是解答的关键.
 (n∈N*),根据对数的运算性质,我们可以求出前n项和为Sn的表达式,解对数不等式可得n的值
(n∈N*),根据对数的运算性质,我们可以求出前n项和为Sn的表达式,解对数不等式可得n的值解答:解:∵an=log2
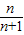
∴Sn=log2
 +log2
+log2 +log2
+log2 +…log2
+…log2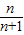 =log2(
=log2( •
• •
• •…•
•…•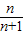 )=log2
)=log2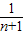
若Sn<-4,则
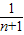
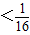
即n>15
则使Sn<-4成立的最小自然数n的值为16
故答案为:16
点评:本题考查的知识点是数列求和,对数的运算性质,对数不等式的解法,其中根据对数的运算性质求出Sn的表达式是解答的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知数列{an}的通项为an=2n-1,Sn为数列{an}的前n项和,令bn=
,则数列{bn}的前n项和的取值范围为( )
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|