题目内容
【题目】如图所示的几何体中,ABC﹣A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°. 
(1)若AA1=AC,求证:AC1⊥平面A1B1CD;
(2)若CD=2,AA1=λAC,二面角A﹣C1D﹣C的余弦值为 ![]() ,求三棱锥C1﹣A1CD的体积.
,求三棱锥C1﹣A1CD的体积.
【答案】
(1)证明:连接A1C交AC1于E,因为AA1=AC,又A A1⊥平面ABCD,所以AA1⊥AC,
所以A1ACC1为正方形,所以A1C⊥AC1,
在△ACD中,AD=2CD,∠ADC=60°,由余弦定理得 AC2=AD2+CD2﹣2 ACDCcos60°,
所以 ![]() ,所以AD2=AC2+CD2,
,所以AD2=AC2+CD2,
所以CD⊥AC,又AA1⊥CD.所以CD⊥平面A1ACC1,
所以CD⊥AC1,所以AC1⊥平面A1 B1CD.
(2)如图建立直角坐标系,则D(2,0,0), ![]() ,
, ![]() ,
, ![]() ∴
∴ ![]() ,
, ![]()
对平面 AC1D,因为 ![]() ,
, ![]()
所以法向量 ![]() ,
,
平面C1CD的法向量为 ![]() ,
,
由 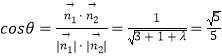 ,得λ=1,
,得λ=1,
所以 A A1=AC,此时,CD=2, ![]() ,
,
所以 ![]()

【解析】(1)连接A1C交AC1于E,证明AA1⊥AC,CD⊥AC,推出CD⊥平面A1ACC1 , 然后证明AC1⊥平面A1 B1CD.(2)如图建立直角坐标系,求出相关点的坐标,求出平面 AC1D的法向量 ![]() ,平面C1CD的法向量为
,平面C1CD的法向量为 ![]() ,通过向量的数量积求出λ=1,然后利用等体积法求解体积即可.
,通过向量的数量积求出λ=1,然后利用等体积法求解体积即可.
【考点精析】关于本题考查的直线与平面垂直的判定,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.

【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪70元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成5元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到如表频数表: 甲公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 20 | 40 | 20 | 10 | 10 |
乙公司送餐员送餐单数频数表
送餐单数 | 38 | 39 | 40 | 41 | 42 |
天数 | 10 | 20 | 20 | 40 | 10 |
(Ⅰ)现从甲公司记录的100天中随机抽取两天,求这两天送餐单数都大于40的概率;
(Ⅱ)若将频率视为概率,回答下列问题:
(i)记乙公司送餐员日工资为X(单位:元),求X的分布列和数学期望;
(ii)小明拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.
【题目】某商品要了解年广告费![]() (单位:万元)对年利润
(单位:万元)对年利润![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年利润
和年利润![]() 数据作了初步整理,得到下面的表格:
数据作了初步整理,得到下面的表格:
广告费 | 2 | 3 | 4 | 5 |
年利润 | 26 | 39 | 49 | 54 |
(Ⅰ)用广告费作解释变量,年利润作预报变量,建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)根据(Ⅰ)的结果预报广告费用为6万元时的年利润.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
