Question

平行四边形ABCD的两条对角线AC、BD交于点M，且

AB

=

a

 ， 

AD

=

b

，则

MB

=（　　）

• A．-

  1

  2

   

  a

  -

  1

  2

   

  b

• B．

  1

  2

   

  a

  +

  1

  2

   

  b

• C．

  1

  2

   

  a

  -

  1

  2

   

  b

• D．-

  1

  2

   

  a

  +

  1

  2

   

  b

Answer 1

分析：由已知中平行四边形ABCD的两条对角线AC、BD交于点M，可得

MB

=

1

2

DB

=

1

2

（

AB

-

AD

），结合

AB

=

a

 ， 

AD

=

b

，可得答案．

解答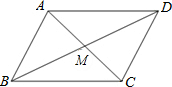：解：∵平行四边形ABCD的两条对角线AC、BD交于点M，
∴M是BD的中点
∴

MB

=

1

2

DB

=

1

2

（

AB

-

AD

）
又∵

AB

=

a

 ， 

AD

=

b

，
∴

MB

=

1

2

a

-

1

2

b

故选C

点评：本题考查的知识点是向量减法运算的三角形法则，其中根据平行四边形的性质，判断出M是BD的中点，进而

MB

=

1

2

DB

=

1

2

（

AB

-

AD

），是解答本题的关键．