题目内容
4. 如图,在四棱锥 P-A BCD中,底面 A BCD为正方形,平面 P AD⊥底面 A BCD,点 E在棱 PD上,且 A E⊥PD.
如图,在四棱锥 P-A BCD中,底面 A BCD为正方形,平面 P AD⊥底面 A BCD,点 E在棱 PD上,且 A E⊥PD.(Ⅰ)求证:平面 A B E⊥平面 PCD;
(Ⅱ)已知 PD与底面 A BCD所成角为30°,求二面角 E-AC-D的正切值.
分析 (I)由AB⊥AD,利用面面垂直的性质可得:AB⊥平面PAD,进而得到PD⊥平面ABE,即可证明;
(II)过点E作EF⊥AD,F为垂足,过点F作FG⊥AC,G为垂足,连接EG.利用面面垂直的性质可得:EF⊥平面ABCD,AC⊥EG.可得:∠EGF是二面角 E-AC-D的平面角.再利用直角三角形的边角关系即可得出.
解答 (I)证明:∵平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,AB⊥AD,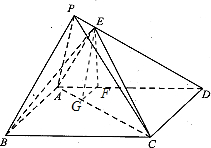
∴AB⊥平面PAD,
∴AB⊥PD,
又AE⊥PD,AB∩AE=A,
∴PD⊥平面ABE,
而PD?平面PCD,
∴平面ABE⊥平面PCD;
(II)解:过点E作EF⊥AD,F为垂足,过点F作FG⊥AC,G为垂足,连接EG.
∵平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,
∴EF⊥平面ABCD,
∴AC⊥EG.
∴∠EGF是二面角 E-AC-D的平面角.
∵PD与底面ABCD所成角为30°,∴∠EDF=30°,
又AE⊥PD,∴∠EAF=60°.
∵tan∠EAF=$\frac{EF}{AF}$,tan∠EGF=$\frac{EF}{FG}$,$\frac{FG}{FA}$=sin45°=$\frac{\sqrt{2}}{2}$.
∴tan∠EGF=$\frac{AF}{FG}tan∠EAD$=$\sqrt{2}tan6{0}^{°}$=$\sqrt{6}$.
∴二面角E-AC-D的正切值为$\sqrt{6}$.
点评 本题考查了线面面面垂直的判定与性质定理、三垂线定理、线面角与二面角、直角三角形的边角关系,考查了空间想象能力、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.在三棱锥S-ABC中,底面是边长为2的正三角形且SA=SB=2,SC=$\sqrt{3}$,则二面角S-AB-C的大小是( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
9.若直线y=-x+1与椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A,B两点,且以AB为直径的圆经过点O(其中O为坐标原点)当椭圆C的离心率e$∈[\frac{1}{2},\frac{\sqrt{3}}{2}]$时椭圆C的长轴长的最大值是( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | 3 | D. | $\frac{3}{2}$ |
 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$.M是AD的中点,P是BM的中点.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$.M是AD的中点,P是BM的中点. 如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,∠BAD=120°,E,F分别为BC,PC的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,∠BAD=120°,E,F分别为BC,PC的中点. 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$. 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=$\sqrt{2}$,AB=BB1=2,∠BCC1=$\frac{π}{4}$,点E在棱BB1上.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=$\sqrt{2}$,AB=BB1=2,∠BCC1=$\frac{π}{4}$,点E在棱BB1上.