题目内容
19．在三棱锥S-ABC中，底面是边长为2的正三角形且SA=SB=2，SC=$\sqrt{3}$，则二面角S-AB-C的大小是（ ）| A． | 90° | B． | 60° | C． | 45° | D． | 30° |
分析 取取AB的中点0，连接OC，SO，则∠SOC是二面角S-AB-C的平面角，结合三角形的边角关系即可得到结论．
解答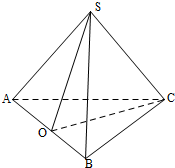 
解：取AB的中点0，
连接OC，SO，
∵底面是边长为2的正三角形且SA=SB=2，
∴SO⊥AB，CO⊥AB，
即∠SOC是二面角S-AB-C的平面角，
则OC=$\sqrt{3}$，S0=$\sqrt{3}$，
即△SOC是正三角形，
则∠SOC=60°，
故选：B．
点评 本题主要考查二面角的求解，根据二面角的定义作出二面角的平面角是解决本题的关键．比较基础．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
已知定点A的坐标是（-4，0），椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{6}}{3}$，F为椭圆的右焦点，M，N两点在椭圆C上，且$\overrightarrow{MF}$=$\overrightarrow{FN}$
如图，在四棱锥 P-A BCD中，底面 A BCD为正方形，平面 P AD⊥底面 A BCD，点 E在棱 PD上，且 A E⊥PD．
如图，已知四边形ABCD是边长为1的正方形，AF⊥平面ABCD，CE⊥平面ABCD．
如图，已知四棱锥P-ABCD，底面是边长为2的正方形，PA⊥底面ABCD，M、N分别为AD、BC的中点，MQ⊥PD于Q，直线PC与平面PBA所成的角的正弦为$\frac{\sqrt{3}}{3}$．