题目内容
12. 如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,∠BAD=120°,E,F分别为BC,PC的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,∠BAD=120°,E,F分别为BC,PC的中点.(1)证明:AE⊥PD
(2)若PA=AB=4,求二面角E-AF-C的余弦值.
分析 (1)由已知条件推导出AE⊥BC,AE⊥AD,由线面垂直得PA⊥AE,由此能证明AE⊥平面PAD,则AE⊥PD;
(2)过E作ES⊥AF于S,连接OS,由已知条件得∠ESO为二面角E-AF-C的平面角,由此能求出二面角E-AF-C的余弦值.
解答 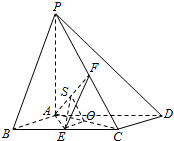 (1)证明:如图,
(1)证明:如图,
由四边形ABCD为菱形,∠BAD=120°,
可得∠ABC=60°,△ABC为正三角形.
∵E为BC的中点,∴AE⊥BC.
又BC∥AD,因此AE⊥AD.
∵PA⊥平面ABCD,AE?平面ABCD,PA⊥AE.
而PA∩AD=A,∴AE⊥平面PAD,
PD?面PAD,∵AE⊥PD;
(2)解:∵PA⊥平面ABCD,PA?平面PAC,∴平面PAC⊥平面ABCD.
过E作EO⊥AC于O,则由面面垂直的性质定理可知:EO⊥平面PAC,
∴EO⊥AF,过E作ES⊥AF于S,连接OS,AF⊥平面ESO,
∴AF⊥SO,则∠ESO为二面角E-AF-C的平面角.
在Rt△AOE中,OE=AEsin30°=$\sqrt{3}$,OA=AEcos30°=3,
又F是PC的中点,PA=AC,∴AF⊥PC且AF=FC,
在Rt△ASO中,SO=AOsin45°=$\frac{3\sqrt{2}}{2}$,
又SE=$\sqrt{E{O}^{2}+S{O}^{2}}$=$\sqrt{\frac{15}{2}}$.
在Rt△ESO中,cosESO=$\frac{OS}{SE}$=$\frac{\sqrt{15}}{5}$.
即二面角E-AF-C的余弦值为$\frac{\sqrt{15}}{5}$.
点评 本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养,是中档题.

练习册系列答案
相关题目
 已知平面α⊥β,且α∩β=l,在l上有两点A,B,线段AC?α,线段BD?β,AC⊥l,BD⊥l,AB=4,AC=3,BD=12,则线段CD的长为13.
已知平面α⊥β,且α∩β=l,在l上有两点A,B,线段AC?α,线段BD?β,AC⊥l,BD⊥l,AB=4,AC=3,BD=12,则线段CD的长为13. 如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形.
如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形.
 如图,在四棱锥 P-A BCD中,底面 A BCD为正方形,平面 P AD⊥底面 A BCD,点 E在棱 PD上,且 A E⊥PD.
如图,在四棱锥 P-A BCD中,底面 A BCD为正方形,平面 P AD⊥底面 A BCD,点 E在棱 PD上,且 A E⊥PD. 如图,在多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,AB∥CD,AD⊥CD,AB=AD=1,CD=2,M、N分别为EC和BD的中点.
如图,在多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,AB∥CD,AD⊥CD,AB=AD=1,CD=2,M、N分别为EC和BD的中点.