题目内容
【题目】对于给定的数列![]() ,
,![]() ,设
,设![]() ,即
,即![]() 是
是![]() ,
,![]() ,…,
,…,![]() 中的最大值,则称数列
中的最大值,则称数列![]() 是数列
是数列![]() ,
,![]() 的“和谐数列”.
的“和谐数列”.
(1)设![]() ,
,![]() ,求
,求![]() ,
,![]() ,
,![]() 的值,并证明数列
的值,并证明数列![]() 是等差数列;
是等差数列;
(2)设数列![]() ,
,![]() 都是公比为q的正项等比数列,若数列
都是公比为q的正项等比数列,若数列![]() 是等差数列,求公比q的取值范围;
是等差数列,求公比q的取值范围;
(3)设数列![]() 满足
满足![]() ,数列
,数列![]() 是数列
是数列![]() ,
,![]() 的“和谐数列”,且
的“和谐数列”,且![]() (m为常数,
(m为常数,![]() ,2,…,k),求证:
,2,…,k),求证:![]() .
.
【答案】(1)![]() ,
,![]() ,
,![]() ;证明详见解析;(2)
;证明详见解析;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)根据和谐数列定义求出![]() ,
,![]() ,
,![]() ,求出
,求出![]() ,利用等差数列定义证明即可;
,利用等差数列定义证明即可;
(2)分![]() 和
和![]() 两种情况讨论,
两种情况讨论,![]() 时,可得
时,可得![]() ,计算
,计算![]() 知数列不是等差数列,当
知数列不是等差数列,当![]() 时,
时,![]() 可满足
可满足![]() 是等差数列;
是等差数列;
(3)根据条件可证明![]() ,可得
,可得![]() ,所以
,所以![]() ,即证
,即证![]() .
.
(1)由题意知![]() ,
,
![]() ,
,
![]()
![]() .
.
因为![]() 恒成立,
恒成立,
所以![]() ,
,
则![]() 4,
4,
即![]() ,
,
故![]() (与n无关的常数),
(与n无关的常数),
所以数列![]() 是公差为1的等差数列.
是公差为1的等差数列.
(2)因为数列![]() ,
,![]() 都是公比为q的正项等比数列,
都是公比为q的正项等比数列,
所以![]() ,
,![]() ,
,![]() .
.
![]() .
.
当![]() 时,
时,![]() ;,
;,
所以![]() ,
,
则![]() .
.
因为![]()
![]()
![]() ,
,
所以![]() ,
,
此时数列![]() 不是等差数列,与题意矛盾.
不是等差数列,与题意矛盾.
当![]() 时,
时,![]() ,
,
所以![]() ,
,
则![]() ,
,
此![]() (与n无关的常数),
(与n无关的常数),
所以数列![]() 是等差数列,符合题意.
是等差数列,符合题意.
综上,公比q的取值范围是![]() .
.
(3)因为![]() ,
,
所以![]() ,
,
上面两式相减得![]()
因为![]()
![]()
![]()
又![]() ,所以
,所以
![]()
![]() ,
,
所以![]()
故![]() ,
,
即![]()
则![]() ,
,
所以![]() .
.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】秉承“绿水青山就是金山银山”的发展理念,某市环保部门通过制定评分标准,先对本市50%的企业进行评估,评出四个等级,并根据等级给予相应的奖惩,如下表所示:
评估得分 |
|
|
|
|
评定等级 | 不合格 | 合格 | 良好 | 优秀 |
奖励(万元) |
| 20 | 40 | 80 |
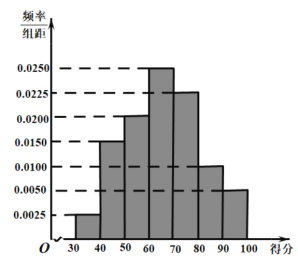
(1)环保部门对企业抽查评估完成后,随机抽取了50家企业的评估得分(![]() 分)为样本,得到如下频率分布表:
分)为样本,得到如下频率分布表:
评估得分 |
|
|
|
|
|
|
频率 | 0.04 | 0.10 |
|
| 0.20 | 0.12 |
其中![]() 、
、![]() 表示模糊不清的两个数字,但知道样本评估得分的平均数是73.6.现从样本外的数百个企业评估得分中随机抽取3个,若以样本中频率为概率,求至少有两家企业的奖励不少于40万元的概率;
表示模糊不清的两个数字,但知道样本评估得分的平均数是73.6.现从样本外的数百个企业评估得分中随机抽取3个,若以样本中频率为概率,求至少有两家企业的奖励不少于40万元的概率;
(2)某企业为取得一个好的得分,在评估前投入80万元进行技术改造,由于技术水平问题,被评定为“合格”“良好”和“优秀”的概率分别为![]() ,
,![]() 和
和![]() ,且由此增加的产值分别为20万元,40万元和60万元.设该企业当年因改造而增加的利润为
,且由此增加的产值分别为20万元,40万元和60万元.设该企业当年因改造而增加的利润为![]() 万元,求
万元,求![]() 的数学期望.
的数学期望.
【题目】在传染病学中,通常把从致病刺激物侵人机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期. 一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
(1)求这1000名患者的潜伏期的样本平均数x (同一组中的数据用该组区间的中点值作代表) ;
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表.请将列联表补充完整,并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
|
| ||
|
| ||
总计 |
|
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立,为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
|
|
|
|
|
|
|
|
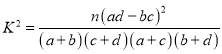 ,其中
,其中![]() .
.