题目内容
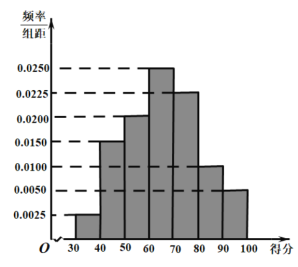
【题目】2020年新冠肺炎疫情暴发以来,中国政府迅速采取最全面、最严格、最彻底的防控举措,坚决遏制疫情蔓延势头,努力把疫情影响降到最低,为全世界抗击新冠肺炎疫情做岀了贡献.为普及防治新冠肺炎的相关知识,某高中学校开展了线上新冠肺炎防控知识竞答活动,现从大批参与者中随机抽取200名幸运者,他们的得分(满分100分)数据统计结果如图:
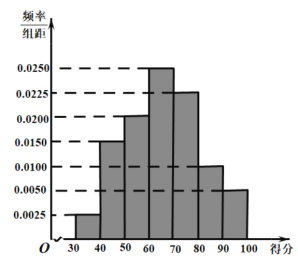
(1)若此次知识竞答得分![]() 整体服从正态分布,用样本来估计总体,设
整体服从正态分布,用样本来估计总体,设![]() ,
,![]() 分别为这200名幸运者得分的平均值和标准差(同一组数据用该区间中点值代替),求
分别为这200名幸运者得分的平均值和标准差(同一组数据用该区间中点值代替),求![]() ,
,![]() 的值(
的值(![]() ,
,![]() 的值四舍五入取整数),并计算
的值四舍五入取整数),并计算![]() ;
;
(2)在(1)的条件下,为感谢大家积极参与这次活动,对参与此次知识竞答的幸运者制定如下奖励方案:得分低于![]() 的获得1次抽奖机会,得分不低于
的获得1次抽奖机会,得分不低于![]() 的获得2次抽奖机会.假定每次抽奖中,抽到18元红包的概率为
的获得2次抽奖机会.假定每次抽奖中,抽到18元红包的概率为![]() ,抽到36元红包的概率为
,抽到36元红包的概率为![]() .已知高三某同学是这次活动中的幸运者,记
.已知高三某同学是这次活动中的幸运者,记![]() 为该同学在抽奖中获得红包的总金额,求
为该同学在抽奖中获得红包的总金额,求![]() 的分布列和数学期望,并估算举办此次活动所需要抽奖红包的总金额.
的分布列和数学期望,并估算举办此次活动所需要抽奖红包的总金额.
参考数据:![]() ;
;![]() ;
;![]() .
.
【答案】(1)![]() ,
,![]() ;
;![]() ;(2)分布列详见解析,数学期望为36;总金额为7200元.
;(2)分布列详见解析,数学期望为36;总金额为7200元.
【解析】
(1)计算![]() ,
,![]() ,故
,故![]() 服从正态分布
服从正态分布![]() ,计算得到答案.
,计算得到答案.
(2)![]() 的取值为18,36,54,72,计算概率得到分布列,再计算数学期望得到答案.
的取值为18,36,54,72,计算概率得到分布列,再计算数学期望得到答案.
(1)![]() ,
,
![]() .即
.即![]() .
.
![]()
![]() .
.
由![]() ,则
,则![]() ,而
,而![]() ,故
,故![]() ,
,
则![]() 服从正态分布
服从正态分布![]() ,
,
![]()
![]() .
.
(2)![]() 的取值为18,36,54,72.
的取值为18,36,54,72.
由题意知,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以![]() 的分布列为
的分布列为
| 18 | 36 | 54 | 72 |
|
|
|
|
|
![]() ,
,
估算所需要抽奖红包的总金额为:![]() (元).
(元).

练习册系列答案
相关题目