题目内容
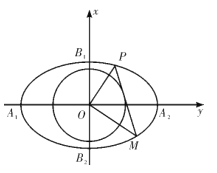
【题目】已知F1、F2是椭圆C：
的左、右焦点，点
在椭圆C上，且满足
.
（1）求椭圆C的方程；
（2）直线l:
交椭圆C于A、B两点，线段AB的垂直平分线与x轴交于点M（t，0），求mt的取值范围.
【答案】（1）
（2）
.
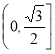【解析】
(1).利用向量数量积得出
,再根据椭圆定义和a,b,c的关系得出方程.
(2).将直线方程与椭圆方程联立,利用韦达定理得出垂直平分线方程,将M点代入直线方程得出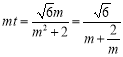
,利用基本不等式得出
的范围,以此得出答案.
（1）.设
，
，由
，得
，.
∴
，
，
∴
，∴
，
，
∴椭圆C的方程为
（2）.由得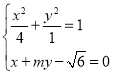
，得
，
，
由
，
且
，得
，
设
，
，则
，
，所以AB的中点为
∵直线AB的斜率为
，∴线段AB的垂直平分线为
.
依题意，
，∴，
∵
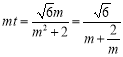，当且仅当
，即
时取等号，
∴
，∴mt的取值范围是
快乐5加2金卷系列答案
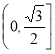
【题目】“一本书，一碗面，一条河，一座桥”曾是兰州的城市名片，而现在“兰州马拉松”又成为了兰州的另一张名片，随着全民运动健康意识的提高，马拉松运动不仅在兰州，而且在全国各大城市逐渐兴起，参与马拉松训练与比赛的人口逐年增加．为此，某市对人们参加马拉松运动的情况进行了统计调查．其中一项调查是调查人员从参与马拉松运动的人中随机抽取200人，对其每周参与马拉松长跑训练的天数进行统计，得到以下统计表：
平均每周进行长跑训练天数 | 不大于2天 | 3天或4天 | 不少于5天 |
人数 | 30 | 130 | 40 |
若某人平均每周进行长跑训练天数不少于5天，则称其为“热烈参与者”，否则称为“非热烈参与者”．
（1）经调查，该市约有2万人参与马拉松运动，试估计其中“热烈参与者”的人数；
（2）根据上表的数据，填写下列2×2列联表，并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“热烈参与马拉松”与性别有关？
热烈参与者 | 非热烈参与者 | 合计 | |
男 | 140 | ||
女 | 55 | ||
合计 |
附：k2=
（n为样本容量）
P（k2≥k0） | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】已知某种细菌的适宜生长温度为10℃～25℃，为了研究该种细菌的繁殖数量
（单位：个）随温度
（单位：℃）变化的规律，收集数据如下：
温度 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
繁殖数量 | 20 | 25 | 33 | 27 | 51 | 112 | 194 |
对数据进行初步处理后，得到了一些统计量的值，如下表所示：
|
|
|
|
|
|
|
18 | 66 | 3.8 | 112 | 4.3 | 1428 | 20.5 |
其中
，
.
（1）请绘出关于的散点图，并根据散点图判断
与
哪一个更适合作为该种细菌的繁殖数量关于温度的回归方程类型（给出判断即可，不必说明理由）；
（2）根据（1）的判断结果及表格数据，建立关于的回归方程（结果精确到0.1）；
（3）当温度为25℃时，该种细菌的繁殖数量的预报值为多少？
参考公式：对于一组数据
，其回归直线
的斜率和截距的最小二成估计分别为
，
.
参考数据：
.
