题目内容
已知函数 在
在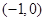 上是增函数.
上是增函数.
⑴求实数 的取值范围
的取值范围 ;
;
⑵当 为
为 中最小值时,定义数列
中最小值时,定义数列 满足:
满足: ,且
,且 ,
,
用数学归纳法证明 ,并判断
,并判断 与
与 的大小.
的大小.
(1)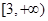 ,(2)
,(2)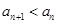 .
.
解析试题分析:(1)本小题即为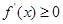 在
在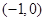 上恒成立,利用分离变量完成此题;(2)用数学归纳法证明时,要注意用到归纳假设
上恒成立,利用分离变量完成此题;(2)用数学归纳法证明时,要注意用到归纳假设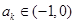 ,对于判断
,对于判断 与
与 的大小可用求差比较法完成.
的大小可用求差比较法完成.
试题解析:⑴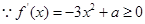 即
即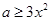 在
在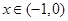 恒成立,
恒成立,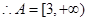 ;
;
⑵用数学归纳法证明: .
.
(ⅰ)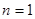 时,由题设
时,由题设 ;
;
(ⅱ)假设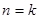 时,
时,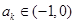 ;则当
;则当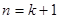 时,
时, ,由⑴知:
,由⑴知: 在
在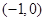 上是增函数,又
上是增函数,又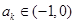 ,所以
,所以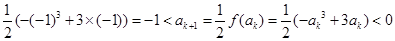 ,综合(ⅰ)(ⅱ)得:对任意
,综合(ⅰ)(ⅱ)得:对任意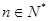 ,
, ,
,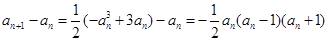 ,因为
,因为 ,所以
,所以 ,即
,即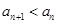 .
.
考点:恒成立问题(分离变量法),数学归纳法,化归思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =
=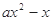 (
( ,
,
 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性; 与
与 的图像有两个不同的交点
的图像有两个不同的交点 ,求
,求 的取值范围。
的取值范围。 和
和 (
( 是函数
是函数 的切线以
的切线以 为切点,求证
为切点,求证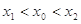 .
. ),试求出此函数的解析式,并写出其定义域,判断奇偶性,单调性.
),试求出此函数的解析式,并写出其定义域,判断奇偶性,单调性. 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为 万元.设余下工程的总费用为
万元.设余下工程的总费用为 万元.
万元. 上恒有f(x)
上恒有f(x)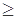 -3成立,求实数a 的取值范围.
-3成立,求实数a 的取值范围. 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
. 的表达式;
的表达式; 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.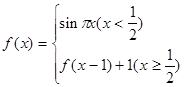 ,求
,求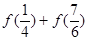 的值。
的值。 ,若关于
,若关于 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是_____▲_____.
的取值范围是_____▲_____.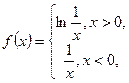 则
则 的解集为________.
的解集为________.