题目内容
【题目】如图所示，一个矩形花园里需要铺两条笔直的小路，已知矩形花园长AD=5m，宽AB=3m，其中一条小路定为AC，另一条小路过点D，问如何在BC上找到一点M，使得两条小路AC与DM相互垂直？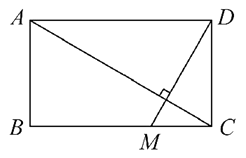
【答案】解: 如图，以点B为坐标原点，BC，BA所在直线分别为x轴，y轴建立直角坐标系.
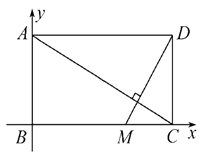
由AD=5m，AB=3m，可得C(5，0)，D(5，3)，A(0，3).
设点M的坐标为(x，0)，
因为AC⊥DM，所以kAC·kDM=-1.
所以 
· 
=-1，即x= 
=3.2，即BM=3.2m时，两条小路AC与DM相互垂直.
【解析】先建立适当的直角坐标系，根据题意可写出点A，B，C，D的坐标，也可以设出点M的坐标，由AC⊥DM可知这两条直线的斜率积为-1，从而可求得点M的坐标，即可确定点M的位置.
云南师大附小一线名师提优作业系列答案
【题目】某车间为了规定工时定额，需要确定加个某零件所花费的时间，为此作了四次实验，得到的数据如下：
零件的个数x（个） | 2 | 3 | 4 | 5 |
加工的时间y（小时） | 2.5 | 3 | 4 | 4.5 |
（1）求出y关于x的线性回归方程；
（2）试预测加工10个零件需要多少时间？
【题目】某单位N名员工参加“社区低碳你我他”活动．他们的年龄在25岁至50岁之间．按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图所示．下表是年龄的频率分布表．
区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50] |
人数 | 25 | a | b |
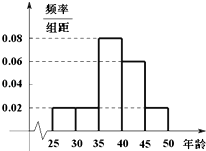
（1）求正整数a，b，N的值；
（2）现要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组的人数分别是多少？
（3）在（2）的条件下，从这6人中随机抽取2人参加社区宣传交流活动，求恰有1人在第3组的概率．
