题目内容
【题目】如图,在直角梯形ABCD中,BC⊥DC , AE⊥DC , M , N分别是AD , BE的中点,将三角形ADE沿AE折起,则下列说法正确的是(填序号).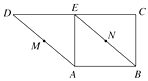
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.
【答案】①②④
【解析】将三角形ADE沿AE折起后几何体如图所示:
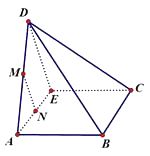
①因为M、N分别是AD、BE的中点,所以不论D折至何位置(不在平面ABC内)都有 ![]() ,
, ![]() 所以①正确;
所以①正确;
② ![]()
![]() ,所以②正确;
,所以②正确;
③ ![]() ,
, ![]() 而
而 ![]() 与
与 ![]() 相交,所以
相交,所以 ![]() 与
与 ![]() 相交,所以③错;
相交,所以③错;
④当 ![]() 时,因为
时,因为 ![]() 平面
平面 ![]() ,所以存在某个位置,使
,所以存在某个位置,使 ![]() ,所以④正确;故答案为①②④.
,所以④正确;故答案为①②④.
根据题意结合已知条件利用中点的性质结合线面平行的判定定理以及线面平行的性质定理即可得到①②正确,再由线面垂直的判定定理以及线面垂直的性质定理即可得出③错④正确。

练习册系列答案
相关题目