题目内容
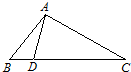
 如图,△ABC中,∠ACB=90°,∠ABC=30°,BC=
如图,△ABC中,∠ACB=90°,∠ABC=30°,BC=| 3 |
分析:图中阴影部分绕直线BC旋转一周所得旋转体的体积,等于一个以AC为底面半径,以BC为高的圆锥的体积,减去一个一个以CN为直径的球,根据已知中,△ABC中,∠ACB=90°,∠ABC=30°,BC=
,代入公式即可得到答案.
| 3 |
解答:解:设半圆的半径为r,在△ABC中,∠ACB=90°,∠ABC=30°,BC=
,
连接OM,则OM⊥AB,
设OM=r,则OB=2r,
因为BC=OC+OB,所以BC=3r,
即r=
.
AC=BC•tan30°=1.
阴影部分绕直线BC旋转一周所得旋转体为底面半径AC=1,高BC=
的圆锥中间挖掉一个半径r=
的球.
所以,V=V圆锥-V球=
•π•12•
-
•π•(
)3=
π.
| 3 |
连接OM,则OM⊥AB,
设OM=r,则OB=2r,
因为BC=OC+OB,所以BC=3r,
即r=
| ||
| 3 |
AC=BC•tan30°=1.
阴影部分绕直线BC旋转一周所得旋转体为底面半径AC=1,高BC=
| 3 |
| ||
| 3 |
所以,V=V圆锥-V球=
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| ||
| 3 |
5
| ||
| 27 |
点评:本题考查的知识点是旋转体的体积,其中根据旋转体的定义判断出图中几何体的形状是解答本题的关键.

练习册系列答案
相关题目
 如图,
如图, 如图,△ABC中,
如图,△ABC中,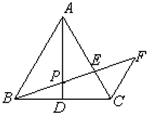 如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F,
如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F, 已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.
已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.