题目内容
 如图,△ABC中,BC=2
如图,△ABC中,BC=2| 3 |
| AB |
| AC |
| AC |
| CB |
(Ⅰ)建立适当的坐标系,求双曲线M的方程;
(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于
F、G两点,直线l的斜率为k,求k的取值范围.;
(Ⅲ)对于(Ⅱ)中的直线l,是否存在k≠0使|OF|=|OG|若有求出k的值,若没有说明理由.(O为原点)
分析:(1)以BC边的中点为原点,BC边所在直线为x轴,建立直角坐标系,则B,C坐标可得,设出A的坐标,进而可表示出
,
和
,进而由
•
=4,
•
=2,求得A点的横坐标和纵坐标,设双曲线方程标准方程,把A坐标代入,以及双曲线的焦距进而求得a和b,双曲线方程可得.
(2)当l⊥x轴时,l与双曲线无交点.当l不垂直x轴时,可设l的方程:y=k(x-1)与双曲线方程联立,消去y,进而根据判别式大于0求得k的范围.
(3)若|OF|=|OG|,三角形OFG中,设M是FG的中点,则有:OM⊥FG,由(2)可求的交点的横坐标之和,进而可表示出中点M的坐标,表示出直线OM和FG的斜率相乘,看结果是不是-1.
| AB |
| AC |
| CB |
| AB |
| AC |
| AC |
| CB |
(2)当l⊥x轴时,l与双曲线无交点.当l不垂直x轴时,可设l的方程:y=k(x-1)与双曲线方程联立,消去y,进而根据判别式大于0求得k的范围.
(3)若|OF|=|OG|,三角形OFG中,设M是FG的中点,则有:OM⊥FG,由(2)可求的交点的横坐标之和,进而可表示出中点M的坐标,表示出直线OM和FG的斜率相乘,看结果是不是-1.
解答: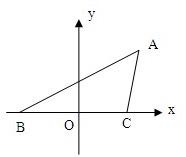 解:(I)以BC边的中点为原点,BC边所在直线为x轴,
解:(I)以BC边的中点为原点,BC边所在直线为x轴,
建立直角坐标系,
则B(-
,0),C(
,0),设A(x0,y0),
故
=(-
-x0,-y0),
=(
-x0,-y0),
=(-2
,0)
由
,得
∴
设双曲线方程为
-
=1(a>0,b>0),又c=
∴
,∴
∴双曲线M的方程为
-y2=1;
(II)当l⊥x轴时,l与双曲线无交点.
当l不垂直x轴时,可设l的方程:y=k(x-1)
由
,消去y,得(1-2k2)x2+4k2x-2(k2+2)=0
∵l与双曲线的左、右两支分别交于F(x1,y1),G(x2,y2),
则
∴-
<k<
(Ⅲ)若|OF|=|OG|,三角形OFG中,设M是FG的中点,
则有:OM⊥FG
由(II)易得x1+x2=
,中点M(
,
)
则应有:KOMKFG=-1,即k•
=-1,显然不成立,
所以不存在这样的k值使|OF|=|OG|.
 解:(I)以BC边的中点为原点,BC边所在直线为x轴,
解:(I)以BC边的中点为原点,BC边所在直线为x轴,建立直角坐标系,
则B(-
| 3 |
| 3 |
故
| AB |
| 3 |
| AC |
| 3 |
| CB |
| 3 |
由
|
|
∴
|
设双曲线方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
∴
|
|
∴双曲线M的方程为
| x2 |
| 2 |
(II)当l⊥x轴时,l与双曲线无交点.
当l不垂直x轴时,可设l的方程:y=k(x-1)
由
|
∵l与双曲线的左、右两支分别交于F(x1,y1),G(x2,y2),
则
|
| ||
| 2 |
| ||
| 2 |
(Ⅲ)若|OF|=|OG|,三角形OFG中,设M是FG的中点,
则有:OM⊥FG
由(II)易得x1+x2=
| 4k2 |
| 2k2-1 |
| 2k2 |
| 2k2-1 |
| k |
| 2k2-1 |
则应有:KOMKFG=-1,即k•
| 1 |
| 2k |
所以不存在这样的k值使|OF|=|OG|.
点评:本题主要考查了双曲线的方程.涉及了直线与双曲线的关系,考查了学生综合分析问题的能力和基本的运算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,△ABC中,
如图,△ABC中,
 已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.
已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.