题目内容
 已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.
已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.求证:AE+CD=AC.
分析:设AD∩CE=0,在AC上取一点F,使CF=CD,由∠B=60°,AD,CE是角平分线,可得∠AOC=120°,进而根据SAS判断出△OFC≌△ODC,结合全等三角形对应角相等可得∠FOC=∠DOC,∠AOE=∠AOF,再由△AOF≌△AOE可得AE=AF,等量代换后,可得答案.
解答: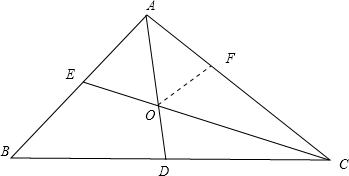 证明:设AD∩CE=0,在AC上取一点F,使CF=CD,
证明:设AD∩CE=0,在AC上取一点F,使CF=CD,
所以∠B=60°,所以∠OAC+∠OCA=60°,∠AOC=120°…..(4分)
因为△OFC≌△ODC,所以∠FOC=∠DOC=60°
得到∠AOE=∠AOF=60°
所以△AOF≌△AOE,得到AE=AF
所以AE+CD=AC…..(10分)
 证明:设AD∩CE=0,在AC上取一点F,使CF=CD,
证明:设AD∩CE=0,在AC上取一点F,使CF=CD,所以∠B=60°,所以∠OAC+∠OCA=60°,∠AOC=120°…..(4分)
因为△OFC≌△ODC,所以∠FOC=∠DOC=60°
得到∠AOE=∠AOF=60°
所以△AOF≌△AOE,得到AE=AF
所以AE+CD=AC…..(10分)
点评:本题考查的知识点是全等三角形的证明与应用,熟练掌握全等三角形的判定定理及性质是解答的关键.

练习册系列答案
相关题目
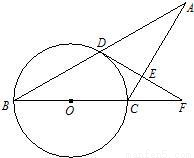
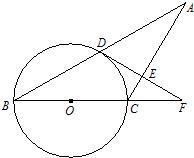 9、已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
9、已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.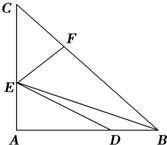 已知:如图,△ABC中,AB=AC,∠BAC=90°,AE=
已知:如图,△ABC中,AB=AC,∠BAC=90°,AE=