题目内容
【题目】如图,在三棱锥![]() 中,顶点
中,顶点![]() 在底面
在底面![]() 上的投影
上的投影![]() 在棱
在棱![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
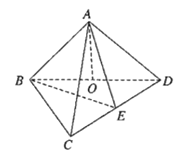
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)已知点![]() 为
为![]() 的中点,在棱
的中点,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)见解析(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)由题知:![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .又根据勾股定理得到
.又根据勾股定理得到![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)首先以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,轴的正方向,建立空间直角坐标系,找到相应点的坐标,再分别求出平面
轴,轴的正方向,建立空间直角坐标系,找到相应点的坐标,再分别求出平面![]() 和平面
和平面![]() 的法向量,带入公式计算即可.
的法向量,带入公式计算即可.
(3)首先设![]() ,
,![]() ,根据
,根据![]() 平面
平面![]() ,得到
,得到![]() ,即可求出
,即可求出![]() ,再计算
,再计算![]() 即可.
即可.
(1)因为顶点![]() 在底面
在底面![]() 上的射影
上的射影![]() 在棱
在棱![]() 上,
上,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
由![]() ,
,![]() ,
,
得![]() ,所以
,所以![]() ,
,
因为![]() 且
且![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
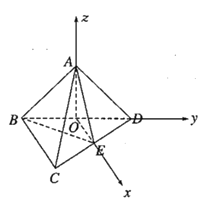
(2)连接![]() ,
,
因为![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,
,
所以![]() ,
,
如图,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,轴的正方向,建立空间直角坐标系,
轴,轴的正方向,建立空间直角坐标系,
![]() ,
,
![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则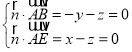 .取
.取![]() ,得
,得![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则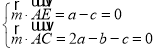 ,取
,取![]() ,则
,则![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)设![]() ,
,![]() ,
,![]()
因为![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.

【题目】某校需从甲、乙两名学生中选一人参加物理竞赛,这两名学生最近5次的物理竞赛模拟成绩如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
学生甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
学生乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(1)根据成绩的稳定性,现从甲、乙两名学生中选出一人参加物理竞赛,你认为选谁比较合适?
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?