题目内容
(1)椭圆C: (a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证:
(a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证: 为定值b2-a2。
为定值b2-a2。
(2)由(1)类比可得如下真命题:双曲线C: (a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则
(a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则 为定值,请写出这个定值(不要求给出解题过程)。
为定值,请写出这个定值(不要求给出解题过程)。
 (a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证:
(a>b>0)与x轴交于A、B两点,点P是椭圆C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,求证: 为定值b2-a2。
为定值b2-a2。(2)由(1)类比可得如下真命题:双曲线C:
 (a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则
(a>0,b>0)与x轴交于A、B两点,点P是双曲线C上异于A、B的任意一点,直线PA、PB分别与y轴交于点M、N,则 为定值,请写出这个定值(不要求给出解题过程)。
为定值,请写出这个定值(不要求给出解题过程)。解:(1)设点P(x0,y0),x0≠±a
依题意,得A(-a,0),B(a,0),
∴直线PA的方程为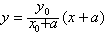
令x=0,得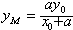
同理可得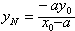
∴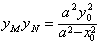
∵点P(x0,y0)是椭圆C上一点
∴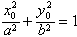
∴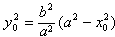
∴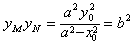
∵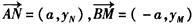
∴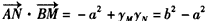 。
。
(2)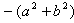 。
。
依题意,得A(-a,0),B(a,0),
∴直线PA的方程为
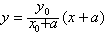
令x=0,得
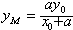
同理可得
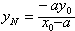
∴
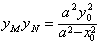
∵点P(x0,y0)是椭圆C上一点
∴
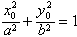
∴
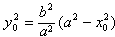
∴
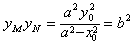
∵
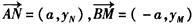
∴
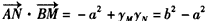 。
。(2)
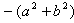 。
。
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 如图,椭圆
如图,椭圆 已知椭圆
已知椭圆