题目内容
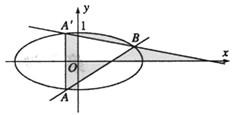 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(l)求椭圆C的方程;
(2)设直线x=my+1与椭圆C交于A,B两点,点A关于x轴的对称点为A′(A′与B不重合),则直线A′B与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
分析:(1)把点(0,1)代入椭圆方程求得a和b的关系,利用离心率求得a和c的关系,进而联立方程求得a和b,则椭圆的方程可得
(2)把直线方程与椭圆方程联立消去y,设出A,B的坐标,则A′的坐标可推断出,利用韦达定理表示出y1+y2和y1y2,进而可表示出A′B的直线方程,把y=0代入求得x的表达式,把x1=my1+1,x2=my2+1代入求得x=4,进而可推断出直线A′B与x轴交于定点(4,0).
(2)把直线方程与椭圆方程联立消去y,设出A,B的坐标,则A′的坐标可推断出,利用韦达定理表示出y1+y2和y1y2,进而可表示出A′B的直线方程,把y=0代入求得x的表达式,把x1=my1+1,x2=my2+1代入求得x=4,进而可推断出直线A′B与x轴交于定点(4,0).
解答:解:(1)依题意可得
,解得a=2,b=1.
所以,椭圆C的方程是
+y2=1;
(2)由
得(my+1)2+4y2=4,即(m2+4)y2+2my-3=0,
设A(x1,y1),B(x2,y2)
则A′(x1,-y1).
且y1+y2=-
,y1y2=-
.
经过点A′(x1,-y1),
B(x2,y2)的直线方程为
=
.
令y=0,则x=
y1+x1=
=
又∵x1=my1+1,x2=my2+1.∴当y=0时,x=
=
=
=4
这说明,直线A′B与x轴交于定点(4,0).
|
所以,椭圆C的方程是
| x2 |
| 4 |
(2)由
|
得(my+1)2+4y2=4,即(m2+4)y2+2my-3=0,
设A(x1,y1),B(x2,y2)
则A′(x1,-y1).
且y1+y2=-
| 2m |
| m2+4 |
| 3 |
| m2+4 |
经过点A′(x1,-y1),
B(x2,y2)的直线方程为
| y+y1 |
| y2+y1 |
| x-x1 |
| x2-x1 |
令y=0,则x=
| x2-x1 |
| y2+y1 |
| (x2-x1)y1+x1(y1+y2) |
| y1+y2 |
| x2y1+x1y2 |
| y1+y2 |
又∵x1=my1+1,x2=my2+1.∴当y=0时,x=
| (my2+1)y1+(my1+1)y2 |
| y1+y2 |
| 2my1y2+(y1+y2) |
| y1+y2 |
-
| ||||
-
|
这说明,直线A′B与x轴交于定点(4,0).
点评:本题主要考查了椭圆的标准方程,直线与椭圆的位置关系.考查了学生基础知识的综合运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
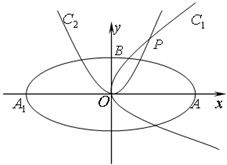 如图,椭圆C:
如图,椭圆C: (2008•闸北区二模)如图,椭圆C:
(2008•闸北区二模)如图,椭圆C: 如图,椭圆
如图,椭圆 如图,椭圆
如图,椭圆 (2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C:
(2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C: