Question

已知椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)经过点（p，q），离心率e=

3

2

．其中p，q分别表示标准正态分布的期望值与标准差．
（1）求椭圆C的方程；
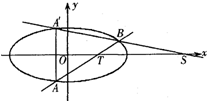
（2）设直线x=my+1与椭圆C交于A，B两点，点A关于x轴的对称点为A'．①试建立△AOB的面积关于m的函数关系；②莆田十中高三（1）班数学兴趣小组通过试验操作初步推断：“当m变化时，直线A'B与x轴交于一个定点”．你认为此推断是否正确？若正确，请写出定点坐标，并证明你的结论；若不正确，请说明理由．

Answer 1

分析：（1）由p，q分别表示标准正态分布的期望值与标准差，可知椭圆过点（0，1），又离心率e=

3

2

，从而可求椭圆C的方程；
（2）①将直线x=my+1与椭圆C联立，易求S=

1

2

|y1-y2| =

2

m2+4

m2+3

； ②取特殊点A′(0，1)，B(

8

5

，

3

5

)，直线A′B：x+4y-4=0与x轴的交点为S（4，0），猜想直线A′B与x轴交于定点S（4，0），再进行证明．

解答：解：（1）依题意椭圆过点（0，1），从而可得

b=1 c a = 3 2 a2=b2+c2

（2分）
解得a=2，b=1．（3分），所以椭圆C的方程是

x2

4

+y2=1．（4分）
（2）①由

x2 4 +y2=1 x=my+1

得（my+1）²+4y²=4，即（m²+4）y²+2my-3=0．（5分）
记A（x₁，y₁），B（x₂，y₂），则A′(x1，-y1)，且y1+y2=-

2m

m2+4

，y1y2=-

3

m2+4

．（6分），易求S=

1

2

|y1-y2| =

2

m2+4

m2+3

（8分）                                         
②特别地，令y₁=-1，则x1=0，m=1，y2=

3

5

此时A′(0，1)，B(

8

5

，

3

5

)，直线A′B：x+4y-4=0与x轴的交点为S（4，0）
若直线A′B与x轴交于一个定点，则定点只能为S（4，0）（9分）
以下证明对于任意的m，直线A′B与x轴交于定点S（4，0）
事实上，经过点A′（x₁，-y₁），B（x₂，y₂）的直线方程为

y+y1

y2+y1

=

x-x1

x2-x1

．
令y=0，得x=

x2-x1

y2+y1

y1+x1．
只需证明

(x2-x1)y1

y2+y1

+x₁=4，（11分）
x₂=my₂+1，x₁=my₁+1
∴即证

m(y2-y1)y1

y2+y1

+my1-3=0，即证2my₁y₂-3（y₁+y₂）=0．
因为2my1y2-3(y1+y2)=

-6m

m2+4

-

-6m

m2+4

=0，所以2my₁y₂-3（y₁+y₂）=0成立．
这说明，当m变化时，直线A′B与x轴交于点S（4，0）（13分）

点评：本题主要考查椭圆标准方程，考查直线与椭圆的位置关系，对于恒过定点问题，通常先猜后证，主要细细体会．