题目内容
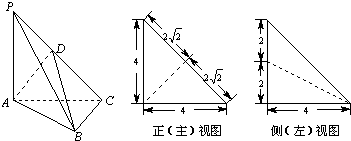
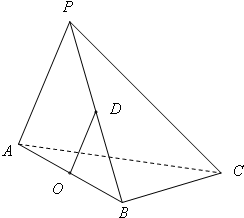 在三棱锥P-ABC中,△PAC和△PBC是边长为
在三棱锥P-ABC中,△PAC和△PBC是边长为| 2 |
(1)求证:OD∥平面PAC;
(2)求证:平面PAB⊥平面ABC;
(3)求三棱锥P-ABC的体积.
分析:(1)欲证OD∥平面PAC,根据直线与平面平行的判定定理可知只需证OD与平面PAC内一直线平行,而OD∥PA,PA?平面PAC,OD?平面PAC,满足定理条件;
(2)欲证平面PAB⊥平面ABC,根据面面垂直的判定定理可知在平面PAB内一直线与平面ABC垂直,而根据题意可得PO⊥平面ABC;
(3)根据OP垂直平面ABC得到OP为三棱锥P-ABC的高,根据三棱锥的体积公式可求出三棱锥P-ABC的体积.
(2)欲证平面PAB⊥平面ABC,根据面面垂直的判定定理可知在平面PAB内一直线与平面ABC垂直,而根据题意可得PO⊥平面ABC;
(3)根据OP垂直平面ABC得到OP为三棱锥P-ABC的高,根据三棱锥的体积公式可求出三棱锥P-ABC的体积.
解答:证明(Ⅰ)∵O,D分别为AB,PB的中点,
∴OD∥PA
又PA?平面PAC,OD?平面PAC
∴OD∥平面PAC.
(Ⅱ)连接OC,OP∵AC=CB=
,O为AB中点,AB=2,
∴OC⊥AB,OC=1.
同理,PO⊥AB,PO=1.
又PC=
,
∴PC2=OC2+PO2=2,
∴∠POC=90°.
∴PO⊥OC.
∵PO⊥OC,PO⊥AB,AB∩OC=O,
∴PO⊥平面ABC.PO?平面PAB
∴平面PAB⊥平面ABC.
解(Ⅲ)由(Ⅱ)可知OP垂直平面ABC,
∴OP为三棱锥P-ABC的高,且OP=1
∴VP-ABC=
S△ABC•OP=
×
×2×1×1=
.
∴OD∥PA
又PA?平面PAC,OD?平面PAC
∴OD∥平面PAC.
(Ⅱ)连接OC,OP∵AC=CB=
| 2 |
∴OC⊥AB,OC=1.
同理,PO⊥AB,PO=1.
又PC=
| 2 |
∴PC2=OC2+PO2=2,
∴∠POC=90°.
∴PO⊥OC.
∵PO⊥OC,PO⊥AB,AB∩OC=O,
∴PO⊥平面ABC.PO?平面PAB
∴平面PAB⊥平面ABC.
解(Ⅲ)由(Ⅱ)可知OP垂直平面ABC,
∴OP为三棱锥P-ABC的高,且OP=1
∴VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题主要考查直线与平面平行的判定,以及平面与平面垂直的判定和三棱锥的体积的计算,体积的求解在最近两年高考中频繁出现,值得重视.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
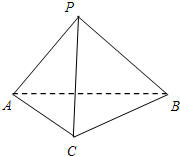 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中, 在三棱锥P-ABC中,AB=3,BC=4,AC=5,PA=1 面PAB⊥面CAB,面PAC⊥面CAB,则三棱锥P-ABC的体积是( )
在三棱锥P-ABC中,AB=3,BC=4,AC=5,PA=1 面PAB⊥面CAB,面PAC⊥面CAB,则三棱锥P-ABC的体积是( )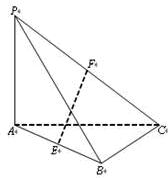 在三棱锥P-ABC中,PA⊥平面ABC.
在三棱锥P-ABC中,PA⊥平面ABC.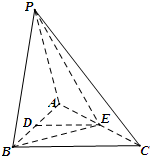 (2013•蚌埠二模)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
(2013•蚌埠二模)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.