题目内容
在实数集R上定义运算:
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若 在R上是减函数,求实数a的取值范围;
在R上是减函数,求实数a的取值范围;
(Ⅲ)若 ,在
,在 的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程;若不存在,说明理由.
的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程;若不存在,说明理由.
【答案】
(I)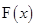
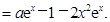 (II)
(II)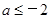 .
.
(III)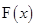 的曲线上不存的两点,使得过这两点的切线点互相垂直.
的曲线上不存的两点,使得过这两点的切线点互相垂直.
【解析】
试题分析:(I)由新定义计算即得,关键是理解“新运算”的意义;
(II)根据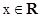 时,
时,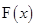 在减函数,得到
在减函数,得到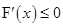 对于
对于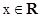 恒成立,
恒成立,
即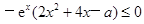 恒成立,得到
恒成立,得到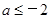 .
.
属于常规题目,难度不大,主要是注意应用“转化与化归思想” .
(III)假定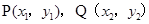 是
是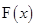 曲线上的任意两点,如果存在互相垂直的切线,则有
曲线上的任意两点,如果存在互相垂直的切线,则有
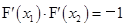 .因此,只需研究
.因此,只需研究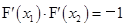 是否成立即可.
是否成立即可.
试题解析:(I)由题意,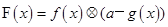 2分
2分
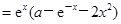
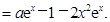 4分
4分
(II)∵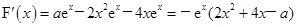 , 6分
, 6分
当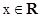 时,
时,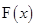 在减函数,
在减函数,
∴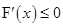 对于
对于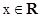 恒成立,即
恒成立,即
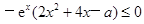 恒成立,
8分
恒成立,
8分
∵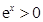 ,
,
∴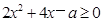 恒成立,
恒成立,
∴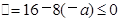 ,
,
∴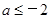 .
9分
.
9分
(III)当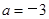 时,
时,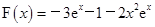 ,
,
设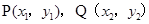 是
是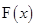 曲线上的任意两点,
曲线上的任意两点,
∵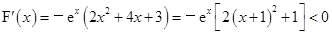 ,
11分
,
11分
∴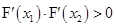 ,
,
∴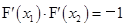 不成立.
12分
不成立.
12分
∴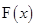 的曲线上不存的两点,使得过这两点的切线点互相垂直. 13分
的曲线上不存的两点,使得过这两点的切线点互相垂直. 13分
考点:新定义,导数的几何意义,应用导数研究函数的单调性

练习册系列答案
相关题目