题目内容
【题目】下列说法正确的是( )
A.将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a倍
B.设有一个回归方程![]() ,变量x增加1个单位时,y平均减少5个单位
,变量x增加1个单位时,y平均减少5个单位
C.线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱
D.在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),则P(ξ>1)=0.5
【答案】BD
【解析】
对A,方差应变为原来的a2倍;对B,x增加1个单位时计算y值与原y值比较可得结论;线性相关系数|r|越大,两个变量的线性相关性越强,反之,线性相关性越弱;根据正态曲线关于x=1对称即可判断.
对于选项A:将一组数据中的每个数据都乘以同一个非零常数a后,方差变为原来的a2倍,故错误.
对于选项B:若有一个回归方程![]() ,变量x增加1个单位时,
,变量x增加1个单位时,![]() ,故y平均减少5个单位,正确.
,故y平均减少5个单位,正确.
对于选项C:线性相关系数|r|越大,两个变量的线性相关性越强;反之,线性相关性越弱,错误.
对于选项D:在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),由于正态曲线关于x=1对称,则P(ξ>1)=0.5,正确.
故选:BD

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: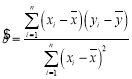 ,
,![]() .
.
【题目】推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度,某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如表:
得分 |
|
|
|
|
|
|
|
男性 人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性 人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率;
(2)将居民对垃圾分类的了解程度分为“比较了解”(得分不低于60分)和“不太了解”(得分低于60分)两类,完成2×2列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
不太了解 | 比较了解 | 合计 | |
男性 | |||
女性 | |||
合计 |
(3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,现从这10人中随机抽取3人作为环保宣传队长,设3人中男性队长的人数为ξ,求ξ的分布列和期望.
附:![]()
![]() ,(n=a+b+c+d).
,(n=a+b+c+d).
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
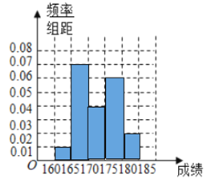
【题目】某大型电器企业,为了解组装车间职工的生活情况,从中随机抽取了![]() 名职工进行测试,得到频数分布表如下:
名职工进行测试,得到频数分布表如下:
日组装个数 |
|
|
|
|
|
|
人数 | 6 | 12 | 34 | 30 | 10 | 8 |
(1)现从参与测试的日组装个数少于![]() 的职工中任意选取
的职工中任意选取![]() 人,求至少有
人,求至少有![]() 人日组装个数少于
人日组装个数少于![]() 的概率;
的概率;
(2)由频数分布表可以认为,此次测试得到的日组装个数![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这
近似为这![]() 人得分的平均值(同一组数据用该组区间的中点值作为代表).
人得分的平均值(同一组数据用该组区间的中点值作为代表).
(![]() 名职工,求日组装个数超过
名职工,求日组装个数超过![]() 的职工人数;
的职工人数;
(ii)为鼓励职工提高技能,企业决定对日组装个数超过![]() 的职工日工资增加
的职工日工资增加![]() 元,若在组装车间所有职工中任意选取
元,若在组装车间所有职工中任意选取![]() 人,求这三人增加的日工资总额的期望.
人,求这三人增加的日工资总额的期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.