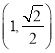Question

【题目】设函数．

（1）当时，讨论函数的单调性；

（2）若时， 恒成立，求整数的最小值．

Answer 1

【答案】(1) f（x）递增区间为（0， ），（1，+∞），递减区间为（，1）；(2)1.

【解析】试题分析：（1）求出函数f（x）的导数，解关于导函数的不等式，求出函数的单调区间即可；
（2）问题转化为a>x-2（x-1）lnx恒成立，令g（x）=x-2（x-1）lnx，根据函数的单调性求出a的最小值即可．

试题解析：

（1）由题意可得f（x）的定义域为（0，+∞），

当a=2时，f（x）=﹣x2+2x+2（x2﹣x）lnx，

所以f′（x）=﹣2x+2+2（2x﹣1）lnx+2（x2﹣x）=（4x﹣2）lnx，

由f'（x）＞0可得：（4x﹣2）lnx＞0，

所以或，

解得x＞1或0＜x＜；

由f'（x）＜0可得：（4x﹣2）lnx＜0，

所以或，

解得：＜x＜1．

综上可知：f（x）递增区间为（0，），（1，+∞），递减区间为（，1）．

（2）若x∈（0，+∞）时，f（x）＞0恒成立，

即a＞x﹣2（x﹣1）lnx恒成立，

令g（x）=x﹣2（x﹣1）lnx，则a＞g（x）max．

因为g′（x）=1﹣2（lnx+）=﹣2lnx﹣1+，

所以g'（x）在（0，+∞）上是减函数，且g'（1）＞0，g′（2）＜0，

故存在x0∈（1，2）使得g（x）在（0，x0）上为增函数，在（x0，+∞）上是减函数，

∴x=x0时，g（x）max=g（x0）≈0，

∴a＞0，又因为a∈Z，所以amin=1．