题目内容
(13分)已知 是定义在
是定义在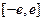 上的奇函数,当
上的奇函数,当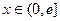 时,
时,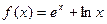 ,其中
,其中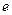 是自然对数的底数.
是自然对数的底数.
(1)求 的解析式;
的解析式;
(2)求 的图象在点
的图象在点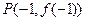 处的切线方程.
处的切线方程.
解:(1)设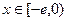 ,则
,则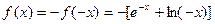 ,又
,又 ,故
,故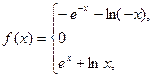
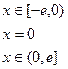
(2)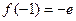 ,故
,故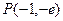 ,当
,当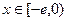 时
时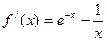 ,
,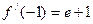
故过点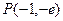 的切线方程为
的切线方程为 ,即
,即
解析

练习册系列答案
相关题目
题目内容
(13分)已知 是定义在
是定义在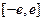 上的奇函数,当
上的奇函数,当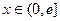 时,
时,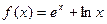 ,其中
,其中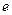 是自然对数的底数.
是自然对数的底数.
(1)求 的解析式;
的解析式;
(2)求 的图象在点
的图象在点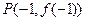 处的切线方程.
处的切线方程.
解:(1)设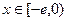 ,则
,则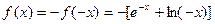 ,又
,又 ,故
,故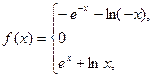
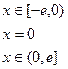
(2)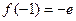 ,故
,故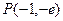 ,当
,当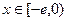 时
时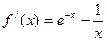 ,
,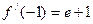
故过点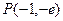 的切线方程为
的切线方程为 ,即
,即
解析
