题目内容
某商店试销某种商品,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 概率 | 0.05 | 0.25 | 0.45 | 0.25 |
(Ⅰ)求当天商品不进货的概率;
(Ⅱ)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望。
(1)0.3 ,(2)X的分布列为X 2 3 4 P 0.25 0.3 0.45
期望EX=3.2
解析试题分析:(1)即指当天出售的件数少于2件 2分 概率P=0.05+0.25=0.3 3分
概率P=0.05+0.25=0.3 3分
(2)X的可能取值为2,3,4 6分
X=2指当天只出售1件,则P(X=2)=0.25
X=3指当天出售0件或3件,则P(X=3)=0.05+0.25=0.3
X=4指当天出售2件,则P(X=4)=0.45 9分 X的分布列为
X的分布列为X 2 3 4 P 0.25 0.3 0.45
期望EX=2×0.25+3×0.3+4×0.45=3.2 12分
考点:本题考查了概率与统计
点评:在求概率时,应注意立事件概率公式的应用,还有区分是属于什么事件.求分布列时要掌握分布列的概念及性质

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
“肇实,正名芡实,因肇庆所产之芡实颗粒大、药力强,故名。”某科研所为进一步改良肇实,为此对肇实的两个品种(分别称为品种A和品种B)进行试验.选取两大片水塘,每大片水塘分成n小片水塘,在总共2n小片水塘中,随机选n小片水塘种植品种A,另外n小片水塘种植B.
(1)假设n=4,在第一大片水塘中,种植品种A的小片水塘的数目记为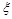 ,求
,求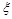 的分布列和数学期望;
的分布列和数学期望;
(2)试验时每大片水塘分成8小片,即n=8,试验结束后得到品种A和品种B在每个小片水塘上的每亩产量(单位:kg/亩)如下表:
| 号码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 品种A | 101 | 97 | 92 | 103 | 91 | 100 | 110 | 106 |
| 品种B | 115 | 107 | 112 | 108 | 111 | 120 | 110 | 113 |
 为摸出两球中白球的个数,
为摸出两球中白球的个数, ,且他们是否译出密码互不影响。
,且他们是否译出密码互不影响。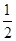 、
、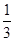 、
、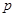 ,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为
,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为 .
.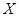 ,求
,求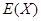 .
. ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为 ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响. ,其中:
,其中: ,记函数
,记函数 满足条件:
满足条件: 的事件为A,求事件A发生的概率。
的事件为A,求事件A发生的概率。
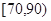 段的有多少人;
段的有多少人; ,出现绿灯的概率都是
,出现绿灯的概率都是 .记这4盏灯中出现红灯的数量为
.记这4盏灯中出现红灯的数量为 ,当这排装饰灯闪烁一次时:
,当这排装饰灯闪烁一次时: 时的概率;(2)求
时的概率;(2)求