题目内容
袋中装有大小相同的2个白球和3个黑球.
(1)采取放回抽样方式,从中依次摸出两个球,求两球颜色不同的概率;
(2)采取不放回抽样方式,从中依次摸出两个球,记 为摸出两球中白球的个数,
为摸出两球中白球的个数,
求 的期望.
的期望.
(1)两球颜色不同的概率是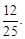 (2)摸出白球个数
(2)摸出白球个数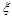 的期望是
的期望是 。
。
解析试题分析:(1)记 “摸出一球,放回后再摸出一个球,两球颜色不同”为事件A,
摸出一球得白球的概率为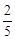 , 摸出一球得黑球的概率为
, 摸出一球得黑球的概率为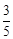 , 3分
, 3分
P(A)=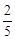 ×
×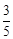 +
+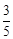 ×
×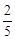 =
=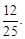
答:两球颜色不同的概率是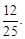 6分
6分
(2)由题知 可取0,1,2, 依题意得 7分
可取0,1,2, 依题意得 7分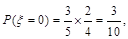
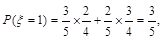
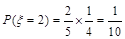 10分
10分
则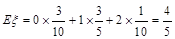 。
。
答: 摸出白球个数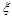 的期望是
的期望是 。. 12分
。. 12分
考点:随机变量的分布列及其数学期望,排列组合计算。
点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。本题对计算能力要求不太高,关键是理解分布列及数学期望的计算方法。

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表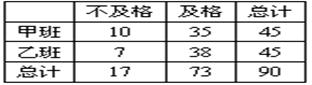
根据表中数据,你有多大把握认为成绩及格与班级有关?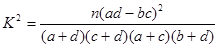
附表:
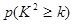 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
某商店试销某种商品,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 概率 | 0.05 | 0.25 | 0.45 | 0.25 |
(Ⅰ)求当天商品不进货的概率;
(Ⅱ)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望。
 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.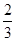 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.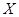 ,求
,求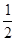 ,
,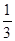 ,
,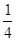 ,记该参加者闯三关所得总分为ζ.
,记该参加者闯三关所得总分为ζ.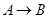 的”闯关”游戏.
的”闯关”游戏. 
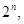 则闯关成功.
则闯关成功. 