题目内容
正方体ABCD-A1B1C1D1 中,点M、N分别在线段AB1、BC1上,且AM=BN.以下结论:①AA1⊥MN;
②MN∥平面A1B1C1D1;
③MN与A1C1异面;
④点B1到面BDC1的距离为
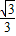 ;⑤若点M、N分别为线段AB1、BC1的中点,则由线MN与AB1确定的平面在正方体ABCD-A1B1C1D1 上的截面为等边三角形.其中有可能成立的结论为 .
;⑤若点M、N分别为线段AB1、BC1的中点,则由线MN与AB1确定的平面在正方体ABCD-A1B1C1D1 上的截面为等边三角形.其中有可能成立的结论为 .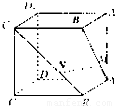
【答案】分析:①作NE⊥BC,MF⊥AB,垂足分别为E,F,可得四边形MNEF是矩形,可得MN∥FE,利用AA1⊥面AC,可得结论成立;
②由①知,MN∥面AC,面AC∥平面A1B1C1D1,故MN∥平面A1B1C1D1;
③MN∥FE,FE与AC所在直线相交时,MN与A1C1异面,;
④根据VB1-BDC1=VD-BB1C1,可求点B1到面BDC1的距离;
⑤截面为△AB1N,为等腰三角形,故⑤不正确.
解答: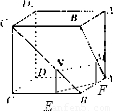 解:①作NE⊥BC,MF⊥AB,垂足分别为E,F,∵AM=BN,∴NE=MF,∴四边形MNEF是矩形,∴MN∥FE,∵AA1⊥面AC,EF?面AC,∴AA1⊥EF,∴AA1⊥MN,故①正确;
解:①作NE⊥BC,MF⊥AB,垂足分别为E,F,∵AM=BN,∴NE=MF,∴四边形MNEF是矩形,∴MN∥FE,∵AA1⊥面AC,EF?面AC,∴AA1⊥EF,∴AA1⊥MN,故①正确;
②由①知,MN∥面AC,面AC∥平面A1B1C1D1,∴MN∥平面A1B1C1D1,故②正确;
③MN∥FE,FE与AC所在直线相交时,MN与A1C1异面,FE与AC平行时,则平行,故③可能成立;
④设正方体ABCD-A1B1C1D1 的棱长为1,点B1到面BDC1的距离为h,根据VB1-BDC1=VD-BB1C1,可得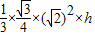 =
= ×
× ×1×1×1,∴h=
×1×1×1,∴h=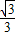 ,故④正确;
,故④正确;
⑤点M、N分别为线段AB1、BC1的中点,则由线MN与AB1确定的平面在正方体ABCD-A1B1C1D1 上的截面为△AB1C,为等腰三角形,故⑤不正确.
综上可知,①②③④
故答案为:①②③④
点评:本题考查线面平行、垂直,考查点到面的距离的计算,考查学生分析解决问题的能力,属于中档题.
②由①知,MN∥面AC,面AC∥平面A1B1C1D1,故MN∥平面A1B1C1D1;
③MN∥FE,FE与AC所在直线相交时,MN与A1C1异面,;
④根据VB1-BDC1=VD-BB1C1,可求点B1到面BDC1的距离;
⑤截面为△AB1N,为等腰三角形,故⑤不正确.
解答:
 解:①作NE⊥BC,MF⊥AB,垂足分别为E,F,∵AM=BN,∴NE=MF,∴四边形MNEF是矩形,∴MN∥FE,∵AA1⊥面AC,EF?面AC,∴AA1⊥EF,∴AA1⊥MN,故①正确;
解:①作NE⊥BC,MF⊥AB,垂足分别为E,F,∵AM=BN,∴NE=MF,∴四边形MNEF是矩形,∴MN∥FE,∵AA1⊥面AC,EF?面AC,∴AA1⊥EF,∴AA1⊥MN,故①正确;②由①知,MN∥面AC,面AC∥平面A1B1C1D1,∴MN∥平面A1B1C1D1,故②正确;
③MN∥FE,FE与AC所在直线相交时,MN与A1C1异面,FE与AC平行时,则平行,故③可能成立;
④设正方体ABCD-A1B1C1D1 的棱长为1,点B1到面BDC1的距离为h,根据VB1-BDC1=VD-BB1C1,可得
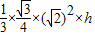 =
= ×
× ×1×1×1,∴h=
×1×1×1,∴h=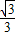 ,故④正确;
,故④正确;⑤点M、N分别为线段AB1、BC1的中点,则由线MN与AB1确定的平面在正方体ABCD-A1B1C1D1 上的截面为△AB1C,为等腰三角形,故⑤不正确.
综上可知,①②③④
故答案为:①②③④
点评:本题考查线面平行、垂直,考查点到面的距离的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的: 已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点. 如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.
如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积. 如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )
如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )