题目内容
【题目】春节期间,受烟花爆竹集中燃放影响,我国多数城市空气中![]() 浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化
浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化![]() 年除夕18时和初一2时,国家环保部门对8个城市空气中
年除夕18时和初一2时,国家环保部门对8个城市空气中![]() 浓度监测的数据如表
浓度监测的数据如表![]() 单位:微克
单位:微克![]() 立方米
立方米![]() .
.
除夕18时 | 初一2时 | |
北京 | 75 | 647 |
天津 | 66 | 400 |
石家庄 | 89 | 375 |
廊坊 | 102 | 399 |
太原 | 46 | 115 |
上海 | 16 | 17 |
南京 | 35 | 44 |
杭州 | 131 | 39 |
![]() Ⅰ
Ⅰ![]() 求这8个城市除夕18时空气中
求这8个城市除夕18时空气中![]() 浓度的平均值;
浓度的平均值;
![]() Ⅱ
Ⅱ![]() 环保部门发现:除夕18时到初一2时空气中
环保部门发现:除夕18时到初一2时空气中![]() 浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹
浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹![]() 从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
![]() Ⅲ
Ⅲ![]() 记2017年除夕18时和初一2时以上8个城市空气中
记2017年除夕18时和初一2时以上8个城市空气中![]() 浓度的方差分别为
浓度的方差分别为![]() 和
和![]() ,比较
,比较![]() 和
和![]() 的大小关系
的大小关系![]() 只需写出结果
只需写出结果![]() .
.
【答案】![]() Ⅰ
Ⅰ![]() 70;
70;![]() Ⅱ
Ⅱ![]() 分布列见解析,
分布列见解析,![]() ;
;![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 利用平均数的计算公式即可得出8个城市除夕18时空气中
利用平均数的计算公式即可得出8个城市除夕18时空气中![]() 浓度的平均值.
浓度的平均值.
![]() 以上8个城市中禁止燃放烟花爆竹的有太原,上海,南京,杭州4个城市,
以上8个城市中禁止燃放烟花爆竹的有太原,上海,南京,杭州4个城市,
随机变量X的所有可能取值为0,1,2,![]() 利用
利用![]() ,即可得出分布列,进而得到X的数学期望
,即可得出分布列,进而得到X的数学期望![]() .
.
![]() 根据数据的集中趋势进行判断即可.
根据数据的集中趋势进行判断即可.
解:![]() Ⅰ
Ⅰ![]() 个城市除夕18时空气中
个城市除夕18时空气中![]() 浓度的平均值
浓度的平均值
![]() .
.
![]() Ⅱ
Ⅱ![]() 以上8个城市中禁止燃放烟花爆竹的有太原,上海,南京,杭州4个城市,
以上8个城市中禁止燃放烟花爆竹的有太原,上海,南京,杭州4个城市,
随机变量X的所有可能取值为0,1,2,![]() ,可得:
,可得:![]() ,
,![]() ,
,![]() ,
,
![]() .
.
X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
X的数学期望![]() .
.
![]() 根据数据的集中趋势进行判断出
根据数据的集中趋势进行判断出![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制如图所示频率分布直方图,已知中间三组的人数可构成等差数列.
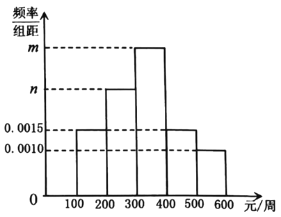
(1)求![]() 的值;
的值;
(2)分析人员对100名调查对象的性别进行统计发现,消费金额不低于300元的男性有20人,低于300元的男性有25人,根据统计数据完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费金额与性别有关?
的把握认为消费金额与性别有关?
(3)分析人员对抽取对象每周的消费金额![]() 与年龄
与年龄![]() 进一步分析,发现他们线性相关,得到回归方程
进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
![]() 列联表
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()