题目内容
(5分)(2011•重庆)若实数a,b,c满足2a+2b=2a+b,2a+2b+2c=2a+b+c,则c的最大值是 .
2﹣log23
试题分析:由基本不等式得2a+2b≥
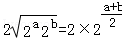 ,可求出2a+b的范围,
,可求出2a+b的范围,再由2a+2b+2c=2a+b+c=2a+b2c=2a+b+2c,2c可用2a+b表达,利用不等式的性质求范围即可.
解:由基本不等式得2a+2b≥
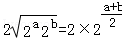 ,即2a+b≥
,即2a+b≥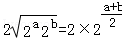 ,所以2a+b≥4,
,所以2a+b≥4,令t=2a+b,由2a+2b+2c=2a+b+c可得2a+b+2c=2a+b2c,所以2c=
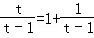
因为t≥4,所以
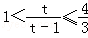 ,即
,即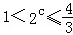 ,所以
,所以
故答案为:2﹣log23
点评:本题考查指数的运算法则,基本不等式求最值、不等式的性质等问题,综合性较强.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
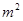 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 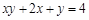 ,则x + y 的最小值为 .
,则x + y 的最小值为 .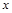 ,
,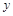 满足
满足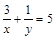 ,则
,则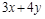 的最小值是( )
的最小值是( )
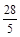
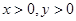 ,若
,若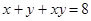 ,则
,则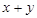 的最小值为 .
的最小值为 .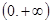 上的函数
上的函数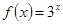 ,若
,若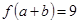 ,则
,则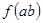 的最大值为______
的最大值为______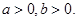 若
若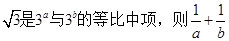 的最小值 ( )
的最小值 ( )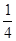
 且
且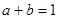 ,则
,则 的最小值为( )
的最小值为( ) 有实根,则实数
有实根,则实数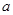 的取值范围是___________.[
的取值范围是___________.[