题目内容
【题目】已知函数
，若曲线
（
为自然对数的底数）上存在点
使得
，则实数
的取值范围为__________.
【答案】
【解析】结合函数的解析式： 
可得：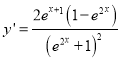 
，
令y′=0，解得：x=0，
当x>0时，y′>0，当x<0，y′<0，
则x∈（-∞，0），函数单调递增，x∈（0，+∞）时，函数y单调递减，
则当x=0时，取最大值，最大值为e，
∴y0的取值范围（0，e]，
结合函数的解析式： 
可得： 
，
x∈（0，e），
，
则f（x）在（0，e）单调递增，
下面证明f（y0）=y0．
假设f（y0）=c>y0，则f（f（y0））=f（c）>f（y0）=c>y0，不满足f（f（y0））=y0．
同理假设f（y0）=c<y0，则不满足f（f（y0））=y0．
综上可得：f（y0）=y0．
令函数
．
设
，求导
，
当x∈（0，e），g′（x）>0，
g（x）在（0，e）单调递增，
当x=e时取最大值，最大值为
，
当x→0时，a→-∞，
∴a的取值范围
.
练习册系列答案
相关题目
