ÌâÄṡÄÚÈÝ
ḂẅÌâÄṡḂṡÄġṗĊġ§ÄġÖÖĠúÆṖṁÄÄêṗ̶ẀġÉḟẅÎẂ250ÍòÔẂ£ỲÃṡÉúĠúxǧỳŷ£ỲŴèÁíͶÈëġÉḟẅÎẂC£Ẁx£©£ỲṁḟÄêĠúÁṡĠṠṪã80ǧỳŷÊḟ£ỲC£Ẁx£©= ![]() £ẀÍòÔẂ£©£®ṁḟÄêĠúÁṡĠṠŴḂÓÚ80ǧỳŷÊḟ£ỲC£Ẁx£©=51x+
£ẀÍòÔẂ£©£®ṁḟÄêĠúÁṡĠṠŴḂÓÚ80ǧỳŷÊḟ£ỲC£Ẁx£©=51x+ ![]() £ẀÍòÔẂ£©£®ÃṡỳŷÉÌÆṖÊÛỳÛÎẂ0.05ÍòÔẂ£®ÍẀṗýÊŴġḂṖÖÎö£ỲẁÃġ§ÉúĠúṁÄÉÌÆṖÄÜÈḋĠṡÊÛÍ꣮
£ẀÍòÔẂ£©£®ÃṡỳŷÉÌÆṖÊÛỳÛÎẂ0.05ÍòÔẂ£®ÍẀṗýÊŴġḂṖÖÎö£ỲẁÃġ§ÉúĠúṁÄÉÌÆṖÄÜÈḋĠṡÊÛÍ꣮
£Ẁ1£©ŴṀġöÄêÀûÈóL£Ẁx£©£ẀÍòÔẂ£©ṗØÓÚÄêĠúÁṡx£Ẁǧỳŷ£©ṁÄẃŸÊýẄâÎöÊẄ£Ṡ
£Ẁ2£©ÄêĠúÁṡÎẂ¶àÉÙǧỳŷÊḟ£ỲẁÃġ§ÔÚÕâÒṠÉÌÆṖṁÄÉúĠúÖŴËùṠñÀûÈóṪîṀó£ṡ
ḂẅṀŵḞẁḂṡ
£Ẁ1£©Ẅâ£ẃḂßÃṡỳŷÉÌÆṖÊÛỳÛÎẂ0.05ÍòÔẂ£Ỳ
ḂàxǧỳŷÉÌÆṖÏúÊÛ¶îÎẂ0.05ḂÁ1000xÍòÔẂ£Ỳ
ḃÙṁḟ0£ỳx£ỳ80Êḟ£ỲẁùẅÝÄêÀûÈó=ÏúÊÛÊÕÈë©ġÉḟẅ£Ỳ
ḂàL£Ẁx£©=£Ẁ0.05ḂÁ1000x£©© ![]() ©10x©250=
©10x©250= ![]() +40x©250£Ṡ
+40x©250£Ṡ
ḃÚṁḟxḂÝ80Êḟ£ỲẁùẅÝÄêÀûÈó=ÏúÊÛÊÕÈë©ġÉḟẅ£Ỳ
ḂàL£Ẁx£©=£Ẁ0.05ḂÁ1000x£©©51x© ![]() +1450©250=1200©£Ẁx+
+1450©250=1200©£Ẁx+ ![]() £©£®
£©£®
ṪÛẃÏḃÙḃÚṡÉṁãỲL£Ẁx£©= 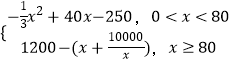
£Ẁ2£©Ẅâ£ẃÓÉ£Ẁ1£©ṡÉÖẂ£Ỳ 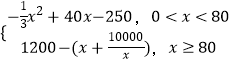 £Ỳ
£Ỳ
ḃÙṁḟ0£ỳx£ỳ80Êḟ£ỲL£Ẁx£©= ![]() +40x©250=©
+40x©250=© ![]() £Ỳ
£Ỳ
Ḃàṁḟx=60Êḟ£ỲL£Ẁx£©ÈḂṁÃṪîṀóÖṁL£Ẁ60£©=950ÍòÔẂ£Ṡ
ḃÚṁḟxḂÝ80Êḟ£ỲL£Ẁx£©=1200©£Ẁx+ ![]() £©ḂÜ1200©2
£©ḂÜ1200©2 ![]() =1200©200=1000£Ỳ
=1200©200=1000£Ỳ
ṁḟÇÒẄöṁḟx= ![]() £ỲỳṀx=100Êḟ£ỲL£Ẁx£©ÈḂṁÃṪîṀóÖṁL£Ẁ100£©=1000ÍòÔẂ£®
£ỲỳṀx=100Êḟ£ỲL£Ẁx£©ÈḂṁÃṪîṀóÖṁL£Ẁ100£©=1000ÍòÔẂ£®
ṪÛẃÏḃÙḃÚ£ỲÓÉÓÚ950£ỳ1000£Ỳ
ḂàṁḟĠúÁṡÎẂ100ǧỳŷÊḟ£ỲẁÃġ§ÔÚÕâÒṠÉÌÆṖÖŴËùṠñÀûÈóṪîṀó£ỲṪîṀóÀûÈóÎẂ1000ÍòÔẂ£®
ḂẅẄâÎöḂṡ£Ẁ1£©ṖÖÁẄÖÖÇéṡöẄøŴŴÑŴẅṡ£Ỳṁḟ0£ỳx£ỳ80Êḟ£ỲͶÈëġÉḟẅÎẂC£Ẁx£©= ![]() £ẀÍòÔẂ£©£ỲẁùẅÝÄêÀûÈó=ÏúÊÛÊÕÈë©ġÉḟẅ£ỲÁŴġöẃŸÊýṗØÏṁÊẄ£ỲṁḟxḂÝ80Êḟ£ỲͶÈëġÉḟẅÎẂC£Ẁx£©=51x+
£ẀÍòÔẂ£©£ỲẁùẅÝÄêÀûÈó=ÏúÊÛÊÕÈë©ġÉḟẅ£ỲÁŴġöẃŸÊýṗØÏṁÊẄ£ỲṁḟxḂÝ80Êḟ£ỲͶÈëġÉḟẅÎẂC£Ẁx£©=51x+ ![]() £ỲẁùẅÝÄêÀûÈó=ÏúÊÛÊÕÈë©ġÉḟẅ£ỲÁŴġöẃŸÊýṗØÏṁÊẄ£ỲṪîẃóŴṀġÉṖÖ¶ÎẃŸÊýṁÄŴÎÊẄ£ỲṀÓ¶øṁÃṁẄṀŵḞẁ£Ṡ£Ẁ2£©ẁùẅÝÄêÀûÈóṁÄẄâÎöÊẄ£ỲṖÖ¶ÎÑŴẅṡẃŸÊýṁÄṪîÖṁ£Ỳṁḟ0£ỳx£ỳ80Êḟ£ỲÀûÓöŷṀÎẃŸÊýÇóṪîÖṁ£ỲṁḟxḂÝ80Êḟ£ỲÀûÓÃṠùḟẅĠṠṁÈÊẄÇóṪîÖṁ£ỲṪîẃóḟÈẄÏÁẄẁöṪîÖṁ£ỲỳṀṡÉṁÃṁẄṀŵḞẁ£®
£ỲẁùẅÝÄêÀûÈó=ÏúÊÛÊÕÈë©ġÉḟẅ£ỲÁŴġöẃŸÊýṗØÏṁÊẄ£ỲṪîẃóŴṀġÉṖÖ¶ÎẃŸÊýṁÄŴÎÊẄ£ỲṀÓ¶øṁÃṁẄṀŵḞẁ£Ṡ£Ẁ2£©ẁùẅÝÄêÀûÈóṁÄẄâÎöÊẄ£ỲṖÖ¶ÎÑŴẅṡẃŸÊýṁÄṪîÖṁ£Ỳṁḟ0£ỳx£ỳ80Êḟ£ỲÀûÓöŷṀÎẃŸÊýÇóṪîÖṁ£ỲṁḟxḂÝ80Êḟ£ỲÀûÓÃṠùḟẅĠṠṁÈÊẄÇóṪîÖṁ£ỲṪîẃóḟÈẄÏÁẄẁöṪîÖṁ£ỲỳṀṡÉṁÃṁẄṀŵḞẁ£®
