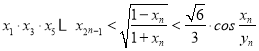题目内容
【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N*,总有b1![]() b2
b2![]() b3…bn﹣1
b3…bn﹣1![]() bn=an+2成立.
bn=an+2成立.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=(﹣1)n![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
【答案】(1)an=2n﹣1,![]() ;(2)
;(2) 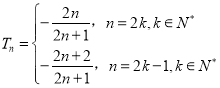 .
.
【解析】
(1)列方程组解等差数列的首项和公差,再求{bn}的通项公式;
(2)裂项![]() ,分奇偶讨论求和.
,分奇偶讨论求和.
(1)设{an}的公差为d,
则a10=a1+9d=19,![]() ,
,
解得a1=1,d=2,所以an=2n﹣1,
所以b1![]() b2
b2![]() b3…bn﹣1
b3…bn﹣1![]() bn=2n+1…①
bn=2n+1…①
当n=1时,b1=3,
当n![]() 2时,b1
2时,b1![]() b2
b2![]() b3…bn﹣1=2n﹣1…②
b3…bn﹣1=2n﹣1…②
①②两式相除得![]()
因为当n=1时,b1=3适合上式,所以![]() .
.
(2)由已知![]() ,
,
得![]()
则Tn=c1+c2+c3+…+cn![]() ,
,
当n为偶数时,![]()
![]()
![]() ,
,
当n为奇数时,![]()
![]()
![]() .
.
综上: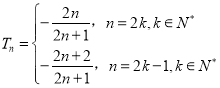 .
.

练习册系列答案
相关题目