题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 与x轴交于A,B两点,点Q的坐标为
与x轴交于A,B两点,点Q的坐标为![]() .
.
(1)是否存在b,使得![]() ,如果存在求出b值;如果不存在,说明理由;
,如果存在求出b值;如果不存在,说明理由;
(2)过A,B,Q三点的圆面积最小时,求圆的方程.
【答案】(1)不存在,理由见详解;(2)![]()
【解析】
(1)求解直线![]() 与直线
与直线![]() 的斜率,根据韦达定理,通过计算斜率之积,即可判断;
的斜率,根据韦达定理,通过计算斜率之积,即可判断;
(2)通过求解![]() 的垂直平分线,求得外接圆圆心坐标,以及半径,再求得半径的最小值,在半径最小的情况下,求得参数
的垂直平分线,求得外接圆圆心坐标,以及半径,再求得半径的最小值,在半径最小的情况下,求得参数![]() ,即可获得圆的方程.
,即可获得圆的方程.
(1)不能出现![]() 的情况,理由如下:
的情况,理由如下:
设![]() ,则
,则![]() 满足
满足![]() ,
,
所以![]() .又Q坐标为
.又Q坐标为![]() .
.
故AQ的斜率与BQ的斜之积为![]()
所以不能出现![]() 的情况.
的情况.
(2)BQ的中点坐标为![]() ,
,
可得BQ的中垂线方程为![]()
由(1)可得![]() ,
,
所以AB的中垂线方程为![]() .
.
联立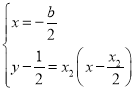 ,
,
又![]() ,可得
,可得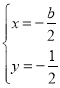
所以过A、B、Q三点的圆的圆心坐标为![]() ,半径
,半径![]() .
.
当![]() 时,半径r最小为
时,半径r最小为![]() ,
,
此时圆的方程为:![]() .
.

练习册系列答案
相关题目
【题目】据气象局统计,某市2019年从1月1日至1月30日这30天里有26天出现雾霾天气.国际上通常用环境空气质量指数(AQI)来描述污染状况,下表是某气象观测点记录的连续4天里,该市AQI指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() 的情况.
的情况.
AQI指数 | 900 | 700 | 300 | 100 |
空气水平可见度 | 0.5 | 3.5 | 6.5 | 9.5 |
(1)设![]() ,根据表中的数据,求出
,根据表中的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)若某天该市AQT指数![]() ,那么当天空气水平可见度大约为多少?
,那么当天空气水平可见度大约为多少?
附:参考数据:![]() ,
,![]() .
.
参考公式:线性回归力程![]() 中,
中,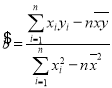 ,
,![]() ,其中
,其中![]() 为样本平均数.
为样本平均数.