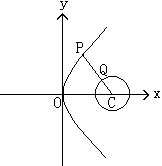题目内容
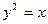
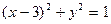
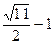
解:设P、Q分别是抛物线和圆上的点,圆心C(3,0),半径为1,若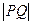 最小,则
最小,则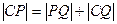 也最小, 因此C、P、Q共线,问题归结为:在抛物线上求一点 P,使它到圆心C的距离最小,为此设
也最小, 因此C、P、Q共线,问题归结为:在抛物线上求一点 P,使它到圆心C的距离最小,为此设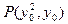 , 则
, 则
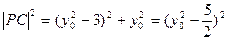
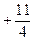
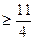 ,
, 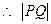 的最小值
的最小值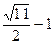 为所
为所
求。
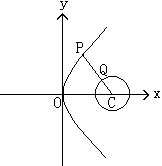
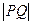 最小,则
最小,则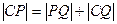 也最小, 因此C、P、Q共线,问题归结为:在抛物线上求一点 P,使它到圆心C的距离最小,为此设
也最小, 因此C、P、Q共线,问题归结为:在抛物线上求一点 P,使它到圆心C的距离最小,为此设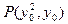 , 则
, 则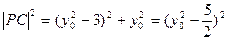
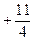
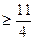 ,
, 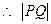 的最小值
的最小值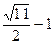 为所
为所求。

练习册系列答案
相关题目
题目内容
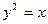
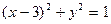
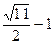
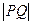 最小,则
最小,则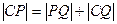 也最小, 因此C、P、Q共线,问题归结为:在抛物线上求一点 P,使它到圆心C的距离最小,为此设
也最小, 因此C、P、Q共线,问题归结为:在抛物线上求一点 P,使它到圆心C的距离最小,为此设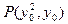 , 则
, 则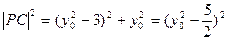
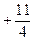
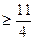 ,
, 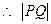 的最小值
的最小值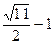 为所
为所