题目内容
已知两点A(-2,0),B(0,2)，点C是圆x2+y2-2x=0上的任意一点，则△ABC的面积最小值是（ ）
A．3- | B．3+ | C． | D． |
A
解析试题分析：A(-2,0),B(0,2)，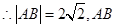
直线方程为
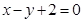，圆x2+y2-2x=0的圆心为
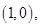半径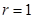
，圆心到直线的距离为
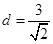，所以圆上的点C到直线的最小距离为
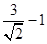，三角形面积最小值为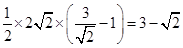
考点：圆的对称性及点到直线距离
点评：要使三角形面积最小需满足动点C到直线AB的距离最小，借助于圆的中心对称性可求得最小距离
练习册系列答案
智能训练练测考系列答案
相关题目
关于函数
有下列命题：
①由
可得
必是
的整数倍；②
的表达式可改写为
；③的图象关于点
对称；④的图象关于直线
对称；⑤在区间
上是增函数；其中正确的是（ ）
| A．②③⑤ | B．①② ③ | C．②③ ④ | D．①③⑤ |
如图，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖位置p(x，y)．若初始位置为P0(
，
)，当秒针从P0（注：此时t=0）正常开始走时，那么点P的纵坐标y与时间t的函数关系为（ ）
A． |
B． |
C． |
D． |
已知函数
在
上单调递增，则正实数ω的取值范围是（ ）
A． | B． | C． | D． |
下列各式中，值为
的是（ ）
A． | B． |
C． | D． |
( )
A． | B． | C．- | D．- |
要得到函数
的导函数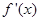
的图象，只需将
的图象（ ）
A．向左平移 个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变） |
B．向左平移个单位，再把各点的纵坐标缩短到原来的 倍（横坐标不变） |
C．向左平移 个单位，再把各点的纵坐标伸长到原来的倍（横坐标不变） |
| D．向左平移个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变） |
下列命题正确的是 （ ）
A．函数 内单调递增 |
B．函数 的最小正周期为2 |
C．函数 的图像是关于点 成中心对称的图形 |
D．函数 的图像是关于直线 成轴对称的图形 |
将函数
后得到函数
（ ）
A． | B． | C． | D． |