题目内容
关于函数 有下列命题:
有下列命题:
①由 可得
可得 必是
必是 的整数倍;②
的整数倍;② 的表达式可改写为
的表达式可改写为 ;③
;③ 的图象关于点
的图象关于点 对称;④
对称;④ 的图象关于直线
的图象关于直线 对称;⑤
对称;⑤ 在区间
在区间 上是增函数;其中正确的是( )
上是增函数;其中正确的是( )
| A.②③⑤ | B.①② ③ | C.②③ ④ | D.①③⑤ |
A
解析试题分析:解:∵ (x∈R)的周期为π,当x1=-
(x∈R)的周期为π,当x1=-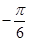 ,x2=
,x2= 时,f(x1)=f(x2)=0,x1-x2 =
时,f(x1)=f(x2)=0,x1-x2 =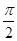 ≠kπ,k∈z,故①是错误的.∵由诱导公式可得f(x)=4sin(2x+
≠kπ,k∈z,故①是错误的.∵由诱导公式可得f(x)=4sin(2x+ )=4cos(
)=4cos(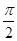 -2x-
-2x- )=4cos(
)=4cos(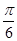 -2x)=4cos(2x-
-2x)=4cos(2x-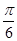 ),故 ②正确.∵当 x=-
),故 ②正确.∵当 x=-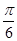 时,f(x)=0,故点(-
时,f(x)=0,故点(-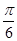 ,0)是f(x)与x轴的交点,故是对称点,故③正确.∵当 x=
,0)是f(x)与x轴的交点,故是对称点,故③正确.∵当 x= 时,f(x)=4sin(2x+
时,f(x)=4sin(2x+ )=0,不是f(x)的最值,故④是错误的.由 2kπ-
)=0,不是f(x)的最值,故④是错误的.由 2kπ-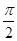 ≤(2x+
≤(2x+ )≤2kπ+
)≤2kπ+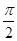 得,kπ-
得,kπ- ≤x≤kπ+
≤x≤kπ+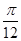 ,k∈z,故⑤正确.综上,②③⑤正确,①④不正确,答案为 A
,k∈z,故⑤正确.综上,②③⑤正确,①④不正确,答案为 A
考点:正弦函数的性质
点评:本题考查正弦函数的对称性、单调性、周期性,诱导公式的应用,熟记正弦函数的性质是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
若函数 的图象(部分)如图所示,则
的图象(部分)如图所示,则 的取值是( )
的取值是( )
A. | B. |
C. | D. |
函数 (x∈R,
(x∈R, >0,0≤
>0,0≤ <2
<2 的部分图象如下图,则
的部分图象如下图,则
A. = = , , = = | B. = = , , = = |
C. = = , , = = | D. = = , , = = |
要得到函数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向右平移 个单位 个单位 | D.向左平移 个单位 个单位 |
设 把
把 的图象按向量
的图象按向量 (
( >0)平移后,恰好得到函数
>0)平移后,恰好得到函数 =
= (
( )的图象,则
)的图象,则 的值可以为( )
的值可以为( )
A. | B. | C.π | D.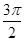 |
已知扇形的半径为2,面积为4,则这个扇形圆心角的弧度数为
A. | B.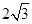 | C. | D.2 |
当 时,函数
时,函数 取得最小值,则函数
取得最小值,则函数
A.是奇函数且图像关于点 对称 对称 | B.是偶函数且图像关于点 对称 对称 |
C.是奇函数且图像关于直线 对称 对称 | D.是偶函数且图像关于直线 对称 对称 |
已知两点A(-2,0),B(0,2),点C是圆x2+y2-2x=0上的任意一点,则△ABC的面积最小值是( )
A.3- | B.3+ | C. | D. |
 ( )
( )
| A.0 | B.1 | C.2 | D.-2 |