题目内容
已知函数
在
上单调递增，则正实数ω的取值范围是（ ）
A． | B． | C． | D． |
A
解析试题分析：由正弦函数的性质，在
时，
是函数的一个单调递增区间，若函数在上单调递增，则
，解得
.故选A.
考点：正弦函数的单调性
点评：本题考查的知识点是正弦型函数的单调性，其中根据正弦型函数的性质，得到ω＞0时，区间
,是函数y=2sinωx的一个单调递增区间，进而结合已知条件构造一个关于ω的不等式组，是解答本题的关键．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
已知
和
都是锐角，且
，
，则
的值是（ ）
A． | B． | C． | D． |
设
把
的图象按向量
(
>0)平移后，恰好得到函数
=
(
)的图象，则的值可以为（ ）
A． | B． | C．π | D． |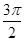
当
时，函数
取得最小值，则函数
A．是奇函数且图像关于点 对称 | B．是偶函数且图像关于点 对称 |
C．是奇函数且图像关于直线 对称 | D．是偶函数且图像关于直线 对称 |
是( )已知两点A(-2,0),B(0,2)，点C是圆x2+y2-2x=0上的任意一点，则△ABC的面积最小值是（ ）
A．3- | B．3+ | C． | D． |
已知
，且
是第二象限角，那么
等于 （ ）
A．－ | B．－ | C． | D． |
已知
，则
化简的结果为 （ ）
A． | B． | C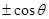． | D．以上都不对 |
一个扇形的圆心角为
，半径为
，则此扇形的面积为（ ）
A． | B． | C． | D． |