题目内容
如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置p(x,y).若初始位置为P0(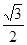 ,
,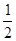 ),当秒针从P0(注:此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系为( )
A. |
B.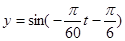 |
C.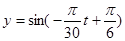 |
D.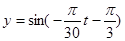 |
C
解析试题分析:先确定函数的周期,再假设函数的解析式,进而可求函数的解析式. 解:由题意,函数的周期为T=60,∴ω=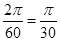 设函数解析式为y=sin(-
设函数解析式为y=sin(-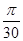 t+φ)(因为秒针是顺时针走动)∵初始位置为P0(
t+φ)(因为秒针是顺时针走动)∵初始位置为P0(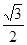 ,
,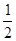 ),∴t=0时,y=
),∴t=0时,y=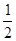 ∴sinφ=
∴sinφ=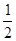 ∴φ可取
∴φ可取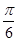 ∴函数解析式为y=sin(-
∴函数解析式为y=sin(-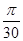 t+
t+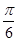 ),故选C.
),故选C.
考点:三角函数解析式
点评:本题考查三角函数解析式的确定,考查学生的阅读能力,解题的关键是确定函数的周期,正确运用初始点的位置.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
若角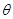 的终边过点P
的终边过点P ,则
,则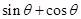 等于 ( )
等于 ( )
A.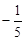 | B.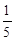 |
C.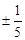 | D.不能确定,与a的值有关 |
要得到函数 的图象,只需将函数
的图象,只需将函数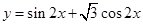 的图象( )
的图象( )
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向右平移 个单位 个单位 | D.向左平移 个单位 个单位 |
已知扇形的半径为2,面积为4,则这个扇形圆心角的弧度数为
A.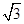 | B.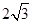 | C.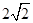 | D.2 |
当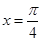 时,函数
时,函数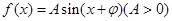 取得最小值,则函数
取得最小值,则函数
A.是奇函数且图像关于点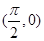 对称 对称 | B.是偶函数且图像关于点 对称 对称 |
C.是奇函数且图像关于直线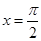 对称 对称 | D.是偶函数且图像关于直线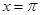 对称 对称 |
若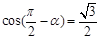 ,则
,则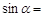 ( ).
( ).
A. | B. | C.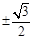 | D.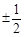 |
已知两点A(-2,0),B(0,2),点C是圆x2+y2-2x=0上的任意一点,则△ABC的面积最小值是( )
A.3-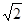 | B.3+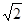 | C.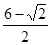 | D.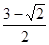 |
函数 是( )
是( )
A.奇函数且在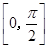 上单调递增 上单调递增 | B.奇函数且在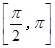 上单调递增 上单调递增 |
C.偶函数且在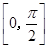 上单调递增 上单调递增 | D.偶函数且在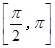 上单调递增 上单调递增 |
已知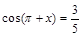 ,
,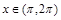 ,则
,则 等于( )
等于( )
A.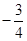 | B.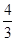 | C.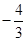 | D.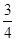 |