题目内容
13.已知函数f(x)=log2(x+a).(1)当a=1时,若0<f(1-2x)-f(x)$<\frac{1}{2}$,求x的取值范围;
(2)若定义在R上的奇函数g(x)满足g(x+2)=-g(x),且当0≤x≤1时,g(x)=f(x),求g(x)在[-3,-1]上的函数表达式;
(3)对于(2)中的g(x),解关于x的不等式g(x)≥1-log23.
分析 (1)利用单调性得出0<log2$\frac{2-2x}{x+1}$$<\frac{1}{2}$,且x>-1,解不等式即可.
(2)利用奇偶性得出a=1,g(x+2)=-g(x),转化得出当0≤x≤1时,g(x)=log2(x+1),当-1≤x≤0时,当-3≤x≤-2,当-2≤x≤-1求解即可.
(3)分类转化不等式为当0≤x≤1时,log2(x+1)≥1-log23,当-1≤x≤0时,-log2(1-x)≥1-log23,当-3≤x≤-2,log2(-x-1))≥1-log23,当-2≤x≤-1,log2(x+3))≥1-log23,分别求解不等式,得出并集即可.
解答 解:(1)∵当a=1时,f(x)=log2(x+1),x>-1
∴f(1-2x)=log2(2-2x),
∵0<f(1-2x)-f(x)$<\frac{1}{2}$,
∴0<log2$\frac{2-2x}{x+1}$$<\frac{1}{2}$,且x>-1,
即1<$\frac{2-2x}{1+x}$$<\sqrt{2}$且x>-1,
求解得出3-2$\sqrt{2}$$<x<\frac{1}{3}$,
故x的取值范围(3-2$\sqrt{2}$,$\frac{1}{3}$)
(2)∵g(x+2)=-g(x),
∴g(x+4)=g(x),
周期为:4,
∵当0≤x≤1时,g(x)=f(x),
∴当0≤x≤1时,g(x)=log2(x+a),
∵定义在R上的奇函数g(x),
∴g(0)=0,即a=1,
∴当0≤x≤1时,g(x)=log2(x+1),
∵当-1≤x≤0时,g(x)=-g(-x)=-log2(1-x),
∴当-1≤x≤0时,g(x)=-log2(1-x),
∵当-3≤x≤-2,则-1≤x+2≤0,g(x+2)=-log2(-x-1)
∴当-3≤x≤-2,g(x)=log2(-x-1)
∵当-2≤x≤-1,则0≤x+2≤1,g(x+2)=log2(x+3)
∴当-2<x≤-1,g(x)=-log2(x+3)
综上g(x)=$\left\{\begin{array}{l}{lo{g}_{2}(-x-1),-3≤x≤-2}\\{-lo{g}_{2}(x+3),-2<x≤-1}\end{array}\right.$.
(3)∵g(x)≥1-log23.
∴当0≤x≤1时,log2(x+1)≥1-log23,解集是[0,1],
当-1≤x≤0时,-log2(1-x)≥1-log23,解集是{x|-$\frac{1}{2}$≤x≤0}
当-3≤x≤-2,log2(-x-1))≥1-log23,解集是{x|-3≤x≤-2}
当-2≤x≤-1,log2(x+3))≥1-log23,解集是[-2,-1].
综上解关于x的不等式g(x)≥1-log23.的解集为:{x|-3≤x≤-1或-$\frac{1}{2}$≤x≤1}
点评 本题考查了对数函数的性质,分类讨论的思想,考查了计算化简能力,属于中档题.

| A. | -1 | B. | -i | C. | 1 | D. | i |
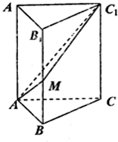 如图,直三棱柱ABCD-A1B1C1中,AB=1,BC=2,AC=$\sqrt{5}$,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,点C到平面AMC1的距离为$\sqrt{3}$.
如图,直三棱柱ABCD-A1B1C1中,AB=1,BC=2,AC=$\sqrt{5}$,AA1=3,M为线段BB1上的一动点,则当AM+MC1最小时,点C到平面AMC1的距离为$\sqrt{3}$.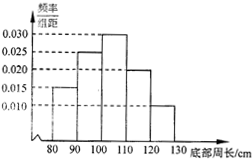 为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.
为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.