题目内容
已知公差不为0的等差数列{an},a1=1,且a2,a4-2,a6成等比数列.
(1)求数列{an}的通项公式;
(2)已知数列{bn}的通项公式是bn=2n-1,集合A={a1,a2,…,an,…},B={b1,b2,b3,…,bn,…}.将集合A∩B中的元素按从小到大的顺序排成一个新的数列{cn},求数列{cn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)已知数列{bn}的通项公式是bn=2n-1,集合A={a1,a2,…,an,…},B={b1,b2,b3,…,bn,…}.将集合A∩B中的元素按从小到大的顺序排成一个新的数列{cn},求数列{cn}的前n项和Sn.
(1)an=3n-2.(2)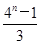
(1)设等差数列{an}的公差为d.
由题意(a4-2)2=a2a6得(3d-1)2=(1+d)(1+5d).
解得d=3或者d=0.因为公差d不为0,所以d=3.
故an=3n-2.
(2)由题意知数列{cn}是数列{an}与数列{bn}的公共项,令2n-1=3m-2,
则2n=2·2n-1=6m-4=3(2m-1)-1不是数列{cn}的项,2n+1=2n-1·22=12m-8=3(4m-2)-2是数列{cn}的项.
所以{cn}是以a1=b1=1为首项,4为公比的等比数列,即
cn=4n-1,
故Sn=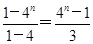 .
.
由题意(a4-2)2=a2a6得(3d-1)2=(1+d)(1+5d).
解得d=3或者d=0.因为公差d不为0,所以d=3.
故an=3n-2.
(2)由题意知数列{cn}是数列{an}与数列{bn}的公共项,令2n-1=3m-2,
则2n=2·2n-1=6m-4=3(2m-1)-1不是数列{cn}的项,2n+1=2n-1·22=12m-8=3(4m-2)-2是数列{cn}的项.
所以{cn}是以a1=b1=1为首项,4为公比的等比数列,即
cn=4n-1,
故Sn=
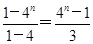 .
.
练习册系列答案
相关题目
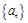 满足
满足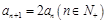 且
且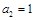 ,则
,则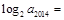 .
. +sinx的所有正的极小值点从小到大排成的数列为{xn}.
+sinx的所有正的极小值点从小到大排成的数列为{xn}.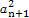 -
-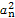 =1(n∈N*),那么使an<5成立的n的最大值为( )
=1(n∈N*),那么使an<5成立的n的最大值为( )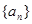 的前
的前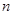 项积为
项积为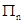 ,若
,若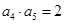 ,则
,则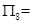 ( )
( )