Question

【题目】对于定义域为的函数，若满足①；②当，且时，都有；③当，且时， ，则称为“偏对称函数”．现给出四个函数：

①； ② ；

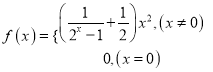③ ； ④．

则其中是“偏对称函数”的函数为__________．

Answer 1

【答案】②④

【解析】由当，且时，都有可得或，即条件②等价于函数在上单调递减，在上单调递增

对于，显然满足①，且易证是偶函数，当时， ，所以在上单调递增，因为是偶函数，所以在上单调递减，满足条件②，由是偶函数可得当，且时， ，故不满足条件③；

对于，显然满足条件①，当时， ，则在上单调递增，当时， ，由复合函数单调性法则可知在上单调递减，故满足条件②，由函数的单调性可知，当时，且时， ，不妨设，则，设，则， 在上单调递减，所以，即，即，所以，即满足条件③；

对于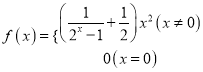，易证是奇函数，由奇函数的性质可得， 在和上的单调性相同，故不满足②；

对于，显然满足条件①， ，则，满足条件②，由的单调性知当时，且时， ，不妨设，则， ，

令，则，当且仅当即时，取等号，所以在上是增函数，所以，即，所以，即，所以，满足条件③；

故答案为②④