题目内容
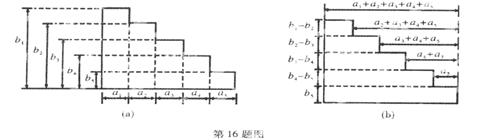
挪威数学家阿贝尔,曾经根据阶梯形图形的两种不同分割(如下图),利用它们的面积关系发现了一个重要的恒等式——阿贝尔公式:
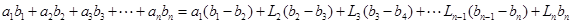
则其中:(I)L3= ;(Ⅱ)Ln= .
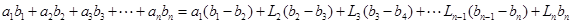

则其中:(I)L3= ;(Ⅱ)Ln= .
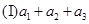 ;
;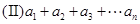 .
.试题分析:由图(b)第三个长方形面积(从上往下数)可知,
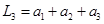 ;对比图(a)与图(b)中最下的长方形面积易知
;对比图(a)与图(b)中最下的长方形面积易知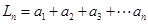 .
.
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
题目内容
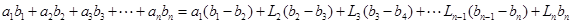

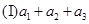 ;
;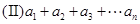 .
.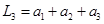 ;对比图(a)与图(b)中最下的长方形面积易知
;对比图(a)与图(b)中最下的长方形面积易知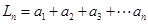 .
.
 口算题天天练系列答案
口算题天天练系列答案