题目内容
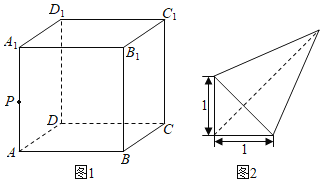
【题目】如图1，已知正方体
的棱长为
，
为棱
的中点，
分别是线段
，
，
上的点，若三棱锥
的俯视图如图2，则三棱锥的体积最大值为（ ）
A.
B.
C.
D.
【答案】D
【解析】
通过俯视图可确定M，Q为所在棱中点，由线面关系可确定当N与C重合时，N到平面PQM的距离最大．由截面图形ACC1A1中的线线关系可知CE，再求出三角形PQM的面积，代入棱锥体积公式求解．
由俯视图知，M为A1D1的中点，Q为A1B1的中点，N为CC1上任意一点，
如图1所示：由中位线可知：PQ∥AB1，MP∥AD1，且
，
，
∴平面PMQ∥平面AB1D1，由正方体中线面关系可知：A1C⊥平面AB1D1，∴A1C⊥平面PMQ，
∴当N与C重合，点N到平面PMQ的距离最大，截面ACC1A1如图2所示，其中平面ACC1A1∩平面PMQ＝PS，
平面ACC1A1∩平面AB1D1＝AT，则
，∴CE＝
，
又A1C＝
，∴最大值为CE＝
A1C＝
＝
．
又
，∴三棱锥P﹣MNQ的体积最大值为
．
故选：D．
图1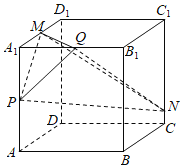
图2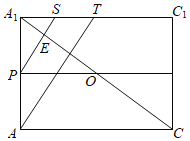 
【题目】某险种的基本保费为a(单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件：“一续保人本年度的保费不高于基本保费”，求P(A)的估计值；
(2)记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”，求P(B)的估计值；
(3)求续保人本年度平均保费的估计值．
【题目】为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样的方法从该地区调查了500位老年人，结果如下：
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附：
的观测值
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（1）估计该地区老年人中，需要志愿者提供帮助的老年人的比例；
（2）在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关？
