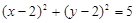题目内容
已知圆C过点A(1,0)和B(3,0),且圆心在直线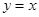 上,则圆C的标准方程为 。
上,则圆C的标准方程为 。
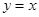 上,则圆C的标准方程为 。
上,则圆C的标准方程为 。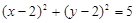
试题分析:根据题意,由于圆C过点A(1,0)和B(3,0),则圆心在直线AB的中垂线x=2上,即为且圆心在直线
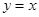 上,故圆心坐标(2,2),半径为A(1,0)与(2,2)两点的距离公式可知为
上,故圆心坐标(2,2),半径为A(1,0)与(2,2)两点的距离公式可知为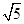 ,因此可知圆的方程为
,因此可知圆的方程为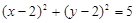
点评:解决的关键是得到圆心和圆的半径,属于基础题。

练习册系列答案
相关题目
题目内容
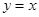 上,则圆C的标准方程为 。
上,则圆C的标准方程为 。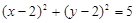
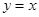 上,故圆心坐标(2,2),半径为A(1,0)与(2,2)两点的距离公式可知为
上,故圆心坐标(2,2),半径为A(1,0)与(2,2)两点的距离公式可知为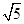 ,因此可知圆的方程为
,因此可知圆的方程为