题目内容
直线l与圆x2+y2=n相切，并且在两坐标轴我的截距之和等于
，则直线l与两坐标轴围成的三角形的面积等于______．
| 3 |
设直线分交x于A（a，0），y轴B（0，b）直线l的斜率大于0
ab＜0 令AB=c
则c2=a2+b2…①
由面积可知c•1=|a•b|…②
因为a+b=
于是（a+b）2=3…③
由①②③可得（ab）2+2ab-3=0
ab=-3或ab=1（舍去），
于是直线l与两坐标轴围成的三角形的面积
s=
|ab|=
故答案为：
．
ab＜0 令AB=c
则c2=a2+b2…①
由面积可知c•1=|a•b|…②
因为a+b=
| 3 |
由①②③可得（ab）2+2ab-3=0
ab=-3或ab=1（舍去），
于是直线l与两坐标轴围成的三角形的面积
s=
| 1 |
| 2 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
练习册系列答案
相关题目
：
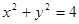和
：
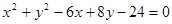的位置关系是 ．
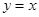上，则圆C的标准方程为 。