题目内容
【题目】设直线![]() 的方程为
的方程为![]() .
.
(1)求证:不论![]() 为何值,直线
为何值,直线![]() 必过一定点
必过一定点![]() ;
;
(2)若直线![]() 分别与
分别与![]() 轴正半轴,
轴正半轴,![]() 轴正半轴交于点
轴正半轴交于点![]() ,
,![]() ,当
,当![]() 而积最小时,求
而积最小时,求![]() 的周长;
的周长;
(3)当直线![]() 在两坐标轴上的截距均为整数时,求直线
在两坐标轴上的截距均为整数时,求直线![]() 的方程.
的方程.
【答案】(1)证明见解析;(2) ![]() ;(3)
;(3) ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)将原式变形为![]() ,由
,由![]() 可得直线
可得直线![]() 必过一定点
必过一定点![]() ;
;
(2)由题可得![]() ,
,![]() ,则
,则![]() ,求出最值,并找到最值的条件,进而可得
,求出最值,并找到最值的条件,进而可得![]() 的周长;
的周长;
(3) ![]() ,
,![]() 均为整数,变形得
均为整数,变形得![]() ,只要
,只要![]() 是整数即可,另外不要漏掉截距为零的情况,求出
是整数即可,另外不要漏掉截距为零的情况,求出![]() ,进而可得直线
,进而可得直线![]() 的方程.
的方程.
解:(1)由![]() 得
得![]() ,
,
则![]() ,解得
,解得![]() ,
,
所以不论![]() 为何值,直线
为何值,直线![]() 必过一定点
必过一定点![]() ;
;
(2)由![]() 得,
得,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
又由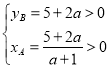 ,得
,得![]() ,
,
![]() ,
,
当且仅当![]() ,即
,即![]() 时,取等号.
时,取等号.
![]() ,
,![]() ,
,
![]() 的周长为
的周长为![]() ;
;
(3) 直线![]() 在两坐标轴上的截距均为整数,
在两坐标轴上的截距均为整数,
即![]() ,
,![]() 均为整数,
均为整数,
![]() ,
,![]() ,
,
又当![]() 时,直线
时,直线![]() 在两坐标轴上的截距均为零,也符合题意,
在两坐标轴上的截距均为零,也符合题意,
所以直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目