题目内容
【题目】在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 的中点.
的中点.
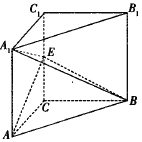
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)根据条件建立空间直角坐标系,设立各点坐标,列方程组解各面法向量,根据向量数量积为零得法向量垂直,即得两平面垂直(2)根据条件建立空间直角坐标系,设立各点坐标,列方程组解各面法向量,根据向量数量积求法向量夹角,最后根据二面角与向量夹角关系确定二面角大小
试题解析:(1)取![]() 中点
中点![]() ,联结
,联结![]() ,
, ![]() ,∵
,∵![]() ,
, ![]() ,
,
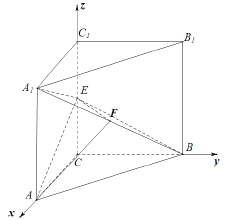
∴![]() ,又∵
,又∵![]() 是直三棱柱,
是直三棱柱,
建立如图空间直角坐标系,根据题意得![]() ,
, ![]() ,
, ![]() ,
, 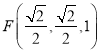 ,
, ![]() ,
,
∴![]() ,
, 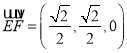 ,
, ![]() ,
,
∴![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)设平面![]() 的法向量为
的法向量为![]() ,则
,则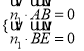 ,即
,即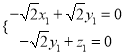 ,
,
令![]() ,则
,则![]() ,
, ![]() ,于是
,于是![]() ,同理,得平面
,同理,得平面![]() 的法向量
的法向量![]() ,
,
∴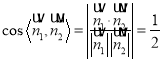 ,即二面角
,即二面角![]() 的余弦值是
的余弦值是![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
【题目】某班主任为了对本班学生的月考成绩进行分析,从全班40名同学中随机抽取一个容量为6的样本进行分析.随机抽取6位同学的数学、物理分数对应如表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学分数x | 60 | 70 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 80 | 88 | 90 | 85 | 95 |
(1)根据上表数据用散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?
(2)如果具有线性相关性,求出线性回归方程(系数精确到0.1);如果不具有线性相关性,请说明理由.
(3)如果班里的某位同学数学成绩为50,请预测这位同学的物理成绩。
![]() (附
(附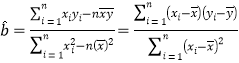 )
)